What is a red-black tree?
A red-black tree is a type of binary search tree that aims to solve a problem that binary search trees (abbreviated BST) seem to have by using some... um... rather complicated algorithms.
So, what are these binary search trees and what problem do they have? A binary search tree is a data structure used for storing data in a way that is very fast. You can search for data quickly, and you can insert and delete data quickly. The term for measuring this quickliness is "asymptotic complexity", "big-O", "big-theta", et cetera et cetera. A BST runs in logarithmic time. You don't need to know what this means to use them other than that "logarithmic time" is rather fast, but I promise that it would be some interesting reading if you do want to look those terms up.
A BST is fast because of the way it stores its data. Say you want to find the 7 in the above BST (remember, BST is short for binary search tree, and I hate typing out that long name). You start at the 5, but 7 is greater than 5, so you go to the right. Then you're at the 8, but 7 is less than 8, so you go left and find it! You visit a total of three nodes (of the 7 in there) to find a value. It may not seem like much, but if you had two million values in that tree, you would still only have to search through at most twenty-one to find one.
Unfortunately, binary search trees have a major problem sometimes. Because of the way they insert things (exactly like finding them), inserting elements 1-2000000 in ascending order messes up the tree. In such a case, it would take two million steps to find the number two million. Trees like this are called "skewed". The first picture of the tree was what is called "balanced".
Balanced trees are better than skewed trees. Unfortunately, unless you're putting data into a BST in random order, you're likely to make it skewed.
Red-black trees solve the skewing problem of BSTs by making sure that the tree is still balanced after every insertion or deletion of data. This extra work that it does after these operations may sound like a bad idea at first, but the work pays off in the long run. The cost of doing the extra work looks like nothing when compared to the speed increase that comes with keeping the tree balanced.
The red-black tree has a set of rules for keeping the tree balanced. First, a node can be either red or black. Second, the root is black. Third, all leaves are the same color as the root. Fourth, both children of every red node must be black. Fifth, every path from a node straight down to any of its decendant leaves has to have the same number of black nodes. (Wikipedia1)
The fourth and fifth rules are the ones that we have to focus on mainly. If you notice in the balanced BST, the height on both sides of any node is the same. The red-black tree forces this setup by rule five. That is why it works.
Unfortunately, keeping the tree perfectly balanced is a real pain and requires too much computing power, and that's where the red nodes come in. The red nodes give us a little bit of leeway in how close to perfectly balanced the tree is. There is rule four, though, that keeps us from abusing this leeway too much.
In this tutorial, you will see many things!
First, I am pretending that all null pointers in nodes actually point to an imaginary node that has no value but is black. Those imaginary nodes are the leaves. This allows us to do things like what is in the picture below.
Second, you will notice that the examples are in C++. I seriously considered using C instead, but I eventually decided that C++ should be used since I'm better at it. The algorithms should be easily converted to any programming language, so have no worries about the language that I'm using.
Third, private and protected data and functions are prepended by an underscore. This is a red flag that something shouldn't be used outside of the code it's designed to work with.
Fourth, you will find an absense of const functions, templates, and other confusing stuff that takes focus away from the matter at hand.
Lastly, if you look really hard, you might find a grammatical error! Please let me know if you do.
Let us begin with the design.
Our red-black tree will have three useful member functions: find, insert, and erase. Also, we will need a testing function to make sure that we are doing everything correctly. To save space in our cpp file, they will all be coded inline.
The public interface functions will be at the bottom of the class declaration, the helper functions will be above those, and the data will be higher still.
The following snippet of code should do for us to start with (and, no, ending a sentence with a preposition does not count as a grammatical mistake).
1 /*
2 * red-black tree example
3 * by Nathan Belue
4 * on April 19, 2011
5 *
6 * Feel free to do whatever you want with this code. If you
7 * choose to edit it, though, please either make a note of the
8 * edit or remove me as an author.
9 *
10 * Also, see my blog post on red-black trees at <http://nathanbelue.blogspot.com/2012/04/red-black-trees.html>
11 */
12
13
14 /*
15 * Included files
16 */
17
18 #include <iostream>
19
20 using namespace std;
21
22
23
24 /*
25 * Some constants and typedefs
26 */
27
28 // The type of data to store
29 typedef int value_type;
30
31 // A constant reference to the type of data to store
32 typedef const value_type & const_reference;
33
34 // I really LOVE C++11's nullptr, but TR1 doesn't support it
35 #if __cplusplus < 201103L
36 #define nullptr 0
37 // ... so now it does
38 #endif
39
40
41
42 /*
43 * For representing colors
44 */
45
46 enum color_type
47 {
48 RED,
49 BLACK
50 };
51
52
53
54 /*
55 * Red-black tree node
56 */
57
58
59 // Our node struct
60 struct rb_node
61 {
62 value_type data;
63 color_type color;
64 rb_node * parent;
65 rb_node * left;
66 rb_node * right;
67 };
68
69 // I don't like typing out pointer types
70 typedef rb_node * node_ptr;
71
72
73
74 /*
75 * Red-black tree class
76 */
77
78 class rb_tree
79 {
80 /*
81 * Data
82 */
83
84 // The root of the tree
85 node_ptr _root;
86
87
88 protected:
89
90 /*
91 * Helper functions
92 */
93
94 //
95
96
97 public:
98
99 /*
100 * Interface functions
101 */
102
103
104 // Constructor
105 rb_tree() : _root(nullptr)
106 {
107 }
108
109
110 // Destructor
111 ~rb_tree()
112 {
113 }
114
115
116 // Find data in the tree
117 // Returns nullptr if not found; otherwise the node that
118 // contains the data.
119 node_ptr find( const_reference value )
120 {
121 }
122
123
124 // Insert data into the tree
125 void insert( const_reference value )
126 {
127 }
128
129
130 // Erase data from the tree
131 void erase( const_reference value )
132 {
133 }
134
135
136 // Make sure that the tree is valid
137 // Throws an error if it isn't.
138 void check()
139 {
140 }
141
142 };
143
144
145
146 /*
147 * Testing section
148 */
149
150
151 // Test insertion
152 // Fills the tree with a lot of random data
153 void test_insertion( rb_tree & tree, int count )
154 {
155 }
156
157
158 // Test erasing
159 // Erases random data from the tree
160 void test_erasing( rb_tree & tree, int count )
161 {
162 }
163
164
165 // Main function
166 int main()
167 {
168 }
170
2 * red-black tree example
3 * by Nathan Belue
4 * on April 19, 2011
5 *
6 * Feel free to do whatever you want with this code. If you
7 * choose to edit it, though, please either make a note of the
8 * edit or remove me as an author.
9 *
10 * Also, see my blog post on red-black trees at <http://nathanbelue.blogspot.com/2012/04/red-black-trees.html>
11 */
12
13
14 /*
15 * Included files
16 */
17
18 #include <iostream>
19
20 using namespace std;
21
22
23
24 /*
25 * Some constants and typedefs
26 */
27
28 // The type of data to store
29 typedef int value_type;
30
31 // A constant reference to the type of data to store
32 typedef const value_type & const_reference;
33
34 // I really LOVE C++11's nullptr, but TR1 doesn't support it
35 #if __cplusplus < 201103L
36 #define nullptr 0
37 // ... so now it does
38 #endif
39
40
41
42 /*
43 * For representing colors
44 */
45
46 enum color_type
47 {
48 RED,
49 BLACK
50 };
51
52
53
54 /*
55 * Red-black tree node
56 */
57
58
59 // Our node struct
60 struct rb_node
61 {
62 value_type data;
63 color_type color;
64 rb_node * parent;
65 rb_node * left;
66 rb_node * right;
67 };
68
69 // I don't like typing out pointer types
70 typedef rb_node * node_ptr;
71
72
73
74 /*
75 * Red-black tree class
76 */
77
78 class rb_tree
79 {
80 /*
81 * Data
82 */
83
84 // The root of the tree
85 node_ptr _root;
86
87
88 protected:
89
90 /*
91 * Helper functions
92 */
93
94 //
95
96
97 public:
98
99 /*
100 * Interface functions
101 */
102
103
104 // Constructor
105 rb_tree() : _root(nullptr)
106 {
107 }
108
109
110 // Destructor
111 ~rb_tree()
112 {
113 }
114
115
116 // Find data in the tree
117 // Returns nullptr if not found; otherwise the node that
118 // contains the data.
119 node_ptr find( const_reference value )
120 {
121 }
122
123
124 // Insert data into the tree
125 void insert( const_reference value )
126 {
127 }
128
129
130 // Erase data from the tree
131 void erase( const_reference value )
132 {
133 }
134
135
136 // Make sure that the tree is valid
137 // Throws an error if it isn't.
138 void check()
139 {
140 }
141
142 };
143
144
145
146 /*
147 * Testing section
148 */
149
150
151 // Test insertion
152 // Fills the tree with a lot of random data
153 void test_insertion( rb_tree & tree, int count )
154 {
155 }
156
157
158 // Test erasing
159 // Erases random data from the tree
160 void test_erasing( rb_tree & tree, int count )
161 {
162 }
163
164
165 // Main function
166 int main()
167 {
168 }
170
You should scan through that and get an idea of how everything will be laid out and used.
Next, let's code the testing code.
Well, we simply want to insert and erase lots of random data, right? We won't worry about the find function since both insert and erase use it and will be testing it pretty thoroughly without our intervention. So, the test_insertion, test_erasing, and main function should look like the following code.
1 // Test insertion
2 // Fills the tree with a lot of random data
3 void test_insertion( rb_tree & tree, int count )
4 {
5 for( int i = 0; i != count; ++i ) {
6 int r = rand() % 3000;
7 tree.insert( r );
8 tree.check();
9 }
10 }
11
12
13 // Test erasing
14 // Erases random data from the tree
15 void test_erasing( rb_tree & tree, int count )
16 {
17 for( int i = 0; i != count; ++i ) {
18 int r = rand() % 3000;
19 tree.erase( r );
20 tree.check();
21 }
22 }
23
24
25 // Main function
26 int main()
27 {
28 try {
29 rb_tree tree;
30 test_insertion( tree, 1000 );
31 test_erasing( tree, 1000 );
32 }
33 catch( const char * e ) {
34 cerr << e << endl;
35 return 1;
36 }
37 }
38
2 // Fills the tree with a lot of random data
3 void test_insertion( rb_tree & tree, int count )
4 {
5 for( int i = 0; i != count; ++i ) {
6 int r = rand() % 3000;
7 tree.insert( r );
8 tree.check();
9 }
10 }
11
12
13 // Test erasing
14 // Erases random data from the tree
15 void test_erasing( rb_tree & tree, int count )
16 {
17 for( int i = 0; i != count; ++i ) {
18 int r = rand() % 3000;
19 tree.erase( r );
20 tree.check();
21 }
22 }
23
24
25 // Main function
26 int main()
27 {
28 try {
29 rb_tree tree;
30 test_insertion( tree, 1000 );
31 test_erasing( tree, 1000 );
32 }
33 catch( const char * e ) {
34 cerr << e << endl;
35 return 1;
36 }
37 }
38
Also, since we are using the rand function, we should include the cstdlib header file. I won't show you that code since it's easy to put in and is only one line.
Next, we need to code rb_tree::check. We need to make sure that the root is black, that the black height on each side of a node is the same, that there are no two red nodes in a row, and that a node's parent points back up to its actual parent.
1 //...
2
3 /*
4 * Helper functions
5 */
6
7
8 // A handy function for getting a node's color
9 // It even works for imaginary leaf nodes!
10 color_type _node_color( node_ptr node )
11 {
12 if( node )
13 return node->color;
14 return BLACK;
15 }
16
17
18 // Check helper function
19 // Returns the black height of a subtree
20 int _check( node_ptr subtree )
21 {
22 // Imaginary leaf? black height is 1
23 if( ! subtree )
24 return 1;
25
26 node_ptr left = subtree->left;
27 node_ptr right = subtree->right;
28
29 // Black height of both sides must be the same
30 int left_height = _check( left );
31 int right_height = _check( right );
32 if( left_height != right_height )
33 throw "black imbalance!";
34
35 // No two reds in a row
36 if( _node_color(subtree) == RED ) {
37 if( _node_color(left) == RED
38 || _node_color(right) == RED )
39 throw "two reds in a row!";
40 }
41
42 // We're black, the height is [left|right]_height + 1
43 else
44 ++ left_height;
45
46 // Make sure that the children's parents are correct
47 if( left && left->parent != subtree
48 || right && right->parent != subtree )
49 throw "parent pointer wrong!";
50
51 // Return our height
52 return left_height;
53 }
54
55
56 public:
57
58 /*
59 * Interface functions
60 */
61
62 // ...
63
64 // Make sure that the tree is valid
65 // Throws an error if it isn't.
66 void check()
67 {
68 if( _node_color(_root) == RED )
69 throw "root is red!";
70
71 _check( _root );
72 }
73
74 };
75
2
3 /*
4 * Helper functions
5 */
6
7
8 // A handy function for getting a node's color
9 // It even works for imaginary leaf nodes!
10 color_type _node_color( node_ptr node )
11 {
12 if( node )
13 return node->color;
14 return BLACK;
15 }
16
17
18 // Check helper function
19 // Returns the black height of a subtree
20 int _check( node_ptr subtree )
21 {
22 // Imaginary leaf? black height is 1
23 if( ! subtree )
24 return 1;
25
26 node_ptr left = subtree->left;
27 node_ptr right = subtree->right;
28
29 // Black height of both sides must be the same
30 int left_height = _check( left );
31 int right_height = _check( right );
32 if( left_height != right_height )
33 throw "black imbalance!";
34
35 // No two reds in a row
36 if( _node_color(subtree) == RED ) {
37 if( _node_color(left) == RED
38 || _node_color(right) == RED )
39 throw "two reds in a row!";
40 }
41
42 // We're black, the height is [left|right]_height + 1
43 else
44 ++ left_height;
45
46 // Make sure that the children's parents are correct
47 if( left && left->parent != subtree
48 || right && right->parent != subtree )
49 throw "parent pointer wrong!";
50
51 // Return our height
52 return left_height;
53 }
54
55
56 public:
57
58 /*
59 * Interface functions
60 */
61
62 // ...
63
64 // Make sure that the tree is valid
65 // Throws an error if it isn't.
66 void check()
67 {
68 if( _node_color(_root) == RED )
69 throw "root is red!";
70
71 _check( _root );
72 }
73
74 };
75
Our check function needed some help, so we coded a recursive _check function and a handy _node_color function. The _node_color works even with those imaginary black leaf nodes.
Next, we need the find function.
I will use an iterative algorithm instead of a recursive algorithm for finding data. Don't worry, it isn't too hard to understand.
1 // Find data in the tree
2 // Returns nullptr if not found; otherwise the node that
3 // contains the data.
4 node_ptr find( const_reference value )
5 {
6 node_ptr node = _root;
7 while( node ) {
8 if( node->data < value )
9 node = node->left;
10 else if( node->data > value )
11 node = node->right;
12 else
13 break;
14 }
15 return node;
16 }
17
2 // Returns nullptr if not found; otherwise the node that
3 // contains the data.
4 node_ptr find( const_reference value )
5 {
6 node_ptr node = _root;
7 while( node ) {
8 if( node->data < value )
9 node = node->left;
10 else if( node->data > value )
11 node = node->right;
12 else
13 break;
14 }
15 return node;
16 }
17
If the value we are looking for is less than the data in the node we are at, then go left; if it is greater, go right. Keep going until we hit a dead-end or we find what we are looking for. That is all that the find function is doing.
Now, we need the destructor coded.
Before we go adding data to the container, we need to code the destructor! It basically clears the entire tree, so why don't we also add a clear interface function just because it's easy? I will use a recursive algorithm for this one because the iterative way is kind of messy. Generally, I hate using recursive algorithms in destructors.
1 // Clear out the data in a subtree
2 void _clear( node_ptr subtree )
3 {
4 if( subtree ) {
5 _clear( subtree->left );
6 _clear( subtree->right );
7 delete subtree;
8 }
9 }
10
11 // ...
12
13
14 public:
15
16 /*
17 * Interface functions
18 */
19
20 // ...
21
22 // Destructor
23 ~rb_tree()
24 {
25 _clear( _root );
26 }
27
28
29 // Clear out the data in the tree
30 void clear()
31 {
32 _clear( _root );
33 _root = nullptr;
34 }
35
2 void _clear( node_ptr subtree )
3 {
4 if( subtree ) {
5 _clear( subtree->left );
6 _clear( subtree->right );
7 delete subtree;
8 }
9 }
10
11 // ...
12
13
14 public:
15
16 /*
17 * Interface functions
18 */
19
20 // ...
21
22 // Destructor
23 ~rb_tree()
24 {
25 _clear( _root );
26 }
27
28
29 // Clear out the data in the tree
30 void clear()
31 {
32 _clear( _root );
33 _root = nullptr;
34 }
35
Finally, we get to the rb-tree code!
What we have so far is the code below. Next, we will start work on the rotation functions and a few other helper functions. After that, we can jump into insertion and then into deletion! Anyways, here is what we have so far:
1 /*
2 * red-black tree example
3 * by Nathan Belue
4 * on April 19, 2011
5 *
6 * Feel free to do whatever you want with this code. If you
7 * choose to edit it, though, please either make a note of the
8 * edit or remove me as an author.
9 *
10 * Also, see my blog post on red-black trees at <http://nathanbelue.blogspot.com/2012/04/red-black-trees.html>
11 */
12
13
14 /*
15 * Included files
16 */
17
18 #include <iostream>
19 #include <cstdlib>
20
21 using namespace std;
22
23
24
25 /*
26 * Some constants and typedefs
27 */
28
29 // The type of data to store
30 typedef int value_type;
31
32 // A constant reference to the type of data to store
33 typedef const value_type & const_reference;
34
35 // I really LOVE C++11's nullptr, but TR1 doesn't support it
36 #if __cplusplus < 201103L
37 #define nullptr 0
38 // ... so now it does
39 #endif
40
41
42
43 /*
44 * For representing colors
45 */
46
47 enum color_type
48 {
49 RED,
50 BLACK
51 };
52
53
54
55 /*
56 * Red-black tree node
57 */
58
59
60 // Our node struct
61 struct rb_node
62 {
63 value_type data;
64 color_type color;
65 rb_node * parent;
66 rb_node * left;
67 rb_node * right;
68 };
69
70 // I don't like typing out pointer types
71 typedef rb_node * node_ptr;
72
73
74
75 /*
76 * Red-black tree class
77 */
78
79 class rb_tree
80 {
81 /*
82 * Data
83 */
84
85 // The root of the tree
86 node_ptr _root;
87
88
89 protected:
90
91
92 /*
93 * Helper functions
94 */
95
96
97 // A handy function for getting a node's color
98 // It even works for imaginary leaf nodes!
99 color_type _node_color( node_ptr node )
100 {
101 if( node )
102 return node->color;
103 return BLACK;
104 }
105
106
107 // Clear out the data in a subtree
108 void _clear( node_ptr subtree )
109 {
110 if( subtree ) {
111 _clear( subtree->left );
112 _clear( subtree->right );
113 delete subtree;
114 }
115 }
116
117
118 // Check helper function
119 // Returns the black height of a subtree
120 int _check( node_ptr subtree )
121 {
122 // Imaginary leaf? black height is 1
123 if( ! subtree )
124 return 1;
125
126 node_ptr left = subtree->left;
127 node_ptr right = subtree->right;
128
129 // Black height of both sides must be the same
130 int left_height = _check( left );
131 int right_height = _check( right );
132 if( left_height != right_height )
133 throw "black imbalance!";
134
135 // No two reds in a row
136 if( _node_color(subtree) == RED ) {
137 if( _node_color(left) == RED
138 || _node_color(right) == RED )
139 throw "two reds in a row!";
140 }
141
142 // Make sure that the children's parents are correct
143 if( left && left->parent != subtree
144 || right && right->parent != subtree )
145 throw "parent pointer wrong!";
146
147 // We're black, the height is [left|right]_height + 1
148 else
149 ++ left_height;
150
151 // Return our height
152 return left_height;
153 }
154
155
156 public:
157
158 /*
159 * Interface functions
160 */
161
162
163 // Constructor
164 rb_tree() : _root(nullptr)
165 {
166 }
167
168
169 // Destructor
170 ~rb_tree()
171 {
172 _clear( _root );
173 }
174
175
176 // Clear out the data in the tree
177 void clear()
178 {
179 _clear( _root );
180 _root = nullptr;
181 }
182
183
184 // Find data in the tree
185 // Returns nullptr if not found; otherwise the node that
186 // contains the data.
187 node_ptr find( const_reference value )
188 {
189 node_ptr node = _root;
190 while( node ) {
191 if( value < node->data )
192 node = node->left;
193 else if( value > node->data )
194 node = node->right;
195 else
196 break;
197 }
198 return node;
199 }
200
201
202 // Insert data into the tree
203 void insert( const_reference value )
204 {
205 }
206
207
208 // Erase data from the tree
209 void erase( const_reference value )
210 {
211 }
212
213
214 // Make sure that the tree is valid
215 // Throws an error if it isn't.
216 void check()
217 {
218 if( _node_color(_root) == RED )
219 throw "root is red!";
220
221 _check( _root );
222 }
223
224 };
225
226
227
228 /*
229 * Testing section
230 */
231
232
233 // Test insertion
234 // Fills the tree with a lot of random data
235 void test_insertion( rb_tree & tree, int count )
236 {
237 for( int i = 0; i != count; ++i ) {
238 int r = rand() % 3000;
239 tree.insert( r );
240 tree.check();
241 }
242 }
243
244
245 // Test erasing
246 // Erases random data from the tree
247 void test_erasing( rb_tree & tree, int count )
248 {
249 for( int i = 0; i != count; ++i ) {
250 int r = rand() % 3000;
251 tree.erase( r );
252 tree.check();
253 }
254 }
255
256
257 // Main function
258 int main()
259 {
260 try {
261 rb_tree tree;
262 test_insertion( tree, 1000 );
263 test_erasing( tree, 1000 );
264 }
265 catch( const char * e ) {
266 cerr << e << endl;
267 return 1;
268 }
269 }
270
2 * red-black tree example
3 * by Nathan Belue
4 * on April 19, 2011
5 *
6 * Feel free to do whatever you want with this code. If you
7 * choose to edit it, though, please either make a note of the
8 * edit or remove me as an author.
9 *
10 * Also, see my blog post on red-black trees at <http://nathanbelue.blogspot.com/2012/04/red-black-trees.html>
11 */
12
13
14 /*
15 * Included files
16 */
17
18 #include <iostream>
19 #include <cstdlib>
20
21 using namespace std;
22
23
24
25 /*
26 * Some constants and typedefs
27 */
28
29 // The type of data to store
30 typedef int value_type;
31
32 // A constant reference to the type of data to store
33 typedef const value_type & const_reference;
34
35 // I really LOVE C++11's nullptr, but TR1 doesn't support it
36 #if __cplusplus < 201103L
37 #define nullptr 0
38 // ... so now it does
39 #endif
40
41
42
43 /*
44 * For representing colors
45 */
46
47 enum color_type
48 {
49 RED,
50 BLACK
51 };
52
53
54
55 /*
56 * Red-black tree node
57 */
58
59
60 // Our node struct
61 struct rb_node
62 {
63 value_type data;
64 color_type color;
65 rb_node * parent;
66 rb_node * left;
67 rb_node * right;
68 };
69
70 // I don't like typing out pointer types
71 typedef rb_node * node_ptr;
72
73
74
75 /*
76 * Red-black tree class
77 */
78
79 class rb_tree
80 {
81 /*
82 * Data
83 */
84
85 // The root of the tree
86 node_ptr _root;
87
88
89 protected:
90
91
92 /*
93 * Helper functions
94 */
95
96
97 // A handy function for getting a node's color
98 // It even works for imaginary leaf nodes!
99 color_type _node_color( node_ptr node )
100 {
101 if( node )
102 return node->color;
103 return BLACK;
104 }
105
106
107 // Clear out the data in a subtree
108 void _clear( node_ptr subtree )
109 {
110 if( subtree ) {
111 _clear( subtree->left );
112 _clear( subtree->right );
113 delete subtree;
114 }
115 }
116
117
118 // Check helper function
119 // Returns the black height of a subtree
120 int _check( node_ptr subtree )
121 {
122 // Imaginary leaf? black height is 1
123 if( ! subtree )
124 return 1;
125
126 node_ptr left = subtree->left;
127 node_ptr right = subtree->right;
128
129 // Black height of both sides must be the same
130 int left_height = _check( left );
131 int right_height = _check( right );
132 if( left_height != right_height )
133 throw "black imbalance!";
134
135 // No two reds in a row
136 if( _node_color(subtree) == RED ) {
137 if( _node_color(left) == RED
138 || _node_color(right) == RED )
139 throw "two reds in a row!";
140 }
141
142 // Make sure that the children's parents are correct
143 if( left && left->parent != subtree
144 || right && right->parent != subtree )
145 throw "parent pointer wrong!";
146
147 // We're black, the height is [left|right]_height + 1
148 else
149 ++ left_height;
150
151 // Return our height
152 return left_height;
153 }
154
155
156 public:
157
158 /*
159 * Interface functions
160 */
161
162
163 // Constructor
164 rb_tree() : _root(nullptr)
165 {
166 }
167
168
169 // Destructor
170 ~rb_tree()
171 {
172 _clear( _root );
173 }
174
175
176 // Clear out the data in the tree
177 void clear()
178 {
179 _clear( _root );
180 _root = nullptr;
181 }
182
183
184 // Find data in the tree
185 // Returns nullptr if not found; otherwise the node that
186 // contains the data.
187 node_ptr find( const_reference value )
188 {
189 node_ptr node = _root;
190 while( node ) {
191 if( value < node->data )
192 node = node->left;
193 else if( value > node->data )
194 node = node->right;
195 else
196 break;
197 }
198 return node;
199 }
200
201
202 // Insert data into the tree
203 void insert( const_reference value )
204 {
205 }
206
207
208 // Erase data from the tree
209 void erase( const_reference value )
210 {
211 }
212
213
214 // Make sure that the tree is valid
215 // Throws an error if it isn't.
216 void check()
217 {
218 if( _node_color(_root) == RED )
219 throw "root is red!";
220
221 _check( _root );
222 }
223
224 };
225
226
227
228 /*
229 * Testing section
230 */
231
232
233 // Test insertion
234 // Fills the tree with a lot of random data
235 void test_insertion( rb_tree & tree, int count )
236 {
237 for( int i = 0; i != count; ++i ) {
238 int r = rand() % 3000;
239 tree.insert( r );
240 tree.check();
241 }
242 }
243
244
245 // Test erasing
246 // Erases random data from the tree
247 void test_erasing( rb_tree & tree, int count )
248 {
249 for( int i = 0; i != count; ++i ) {
250 int r = rand() % 3000;
251 tree.erase( r );
252 tree.check();
253 }
254 }
255
256
257 // Main function
258 int main()
259 {
260 try {
261 rb_tree tree;
262 test_insertion( tree, 1000 );
263 test_erasing( tree, 1000 );
264 }
265 catch( const char * e ) {
266 cerr << e << endl;
267 return 1;
268 }
269 }
270
What are the helper functions that we want? Well, we know that we will need to do tree rotations. And tree rotations are much easier if you have a link to the node (those green lines in the pictures). So, we need the ability to represent those lines, and we need rotation functions.
Lets start with the links, aka the green lines. The implementation is kind of confusing, so we use some functions to deal with that stuff, and all that we need to know is that they are those little green lines! Whenever we set the destination of a link, whatever node the link is coming from now has its little green line pointing to somewhere else.
1 // ...
2
3 /*
4 * Typedefs
5 */
6
7 // A link typedef
8 typedef node_ptr * link_type;
9
10
11 protected:
12
13
14 /*
15 * Helper functions
16 */
17
18 // ...
19
20 // Convert a node pointer to a link
21 // You must pass it something like node->left.
22 // Passing it just node or just left won't work.
23 link_type _make_link( node_ptr & node )
24 {
25 return & node;
26 }
27
28 // Get a node's parent's link to that node
29 link_type _get_parent_link( node_ptr node )
30 {
31 node_ptr parent = node->parent;
32 if( ! parent )
33 return _make_link( _root );
34 if( parent->left == node )
35 return _make_link( parent->left );
36 //if( parent->right == node )
37 return _make_link( parent->right );
38 }
39
40 // Get a link's destination
41 node_ptr _link_dest( link_type link )
42 {
43 return *link;
44 }
45
46 // Set a link's destination
47 void _link_set_dest( link_type link, node_ptr dest )
48 {
49 *link = dest;
50 }
51
52 // Get a link's origin
53 node_ptr _link_orig( link_type link )
54 {
55 return _link_dest(link) -> parent;
56 }
57
2
3 /*
4 * Typedefs
5 */
6
7 // A link typedef
8 typedef node_ptr * link_type;
9
10
11 protected:
12
13
14 /*
15 * Helper functions
16 */
17
18 // ...
19
20 // Convert a node pointer to a link
21 // You must pass it something like node->left.
22 // Passing it just node or just left won't work.
23 link_type _make_link( node_ptr & node )
24 {
25 return & node;
26 }
27
28 // Get a node's parent's link to that node
29 link_type _get_parent_link( node_ptr node )
30 {
31 node_ptr parent = node->parent;
32 if( ! parent )
33 return _make_link( _root );
34 if( parent->left == node )
35 return _make_link( parent->left );
36 //if( parent->right == node )
37 return _make_link( parent->right );
38 }
39
40 // Get a link's destination
41 node_ptr _link_dest( link_type link )
42 {
43 return *link;
44 }
45
46 // Set a link's destination
47 void _link_set_dest( link_type link, node_ptr dest )
48 {
49 *link = dest;
50 }
51
52 // Get a link's origin
53 node_ptr _link_orig( link_type link )
54 {
55 return _link_dest(link) -> parent;
56 }
57
Now let's do the rotations. We will need clockwise rotations and counterclockwise rotations. Usually, they are called right and left rotations, respectfully. I call them clockwise and counterclockwise.
Let's say that we want to rotate the root node counterclockwise. We want to do it, but we also want the nodes to stay in the correct order. Watch. This is how you do it.
And that is how a counterclockwise rotation works! A clockwise rotation is exactly the same idea... just hold the picture up to a mirror. Here is the code for the rotations:
1 /*
2 * Helper functions
3 */
4
5 // ...
6
7 // Rotate about a node counterclockwise
8 void _rotate_counterclockwise( link_type link )
9 {
10 node_ptr node = _link_dest(link);
11 node_ptr right = node->right;
12 node_ptr rleft = right->left;
13
14 _link_set_dest( link, right );
15 right->parent = node->parent;
16
17 right->left = node;
18 node->parent = right;
19
20 node->right = rleft;
21 if( rleft )
22 rleft->parent = node;
23 }
24
25 // Rotate about a node clockwise
26 void _rotate_clockwise( link_type link )
27 {
28 node_ptr node = _link_dest( link );
29 node_ptr left = node->left;
30 node_ptr lright = left->right;
31
32 _link_set_dest( link, left );
33 left->parent = node->parent;
34
35 left->right = node;
36 node->parent = left;
37
38 node->left = lright;
39 if( lright )
40 lright->parent = node;
41 }
42
2 * Helper functions
3 */
4
5 // ...
6
7 // Rotate about a node counterclockwise
8 void _rotate_counterclockwise( link_type link )
9 {
10 node_ptr node = _link_dest(link);
11 node_ptr right = node->right;
12 node_ptr rleft = right->left;
13
14 _link_set_dest( link, right );
15 right->parent = node->parent;
16
17 right->left = node;
18 node->parent = right;
19
20 node->right = rleft;
21 if( rleft )
22 rleft->parent = node;
23 }
24
25 // Rotate about a node clockwise
26 void _rotate_clockwise( link_type link )
27 {
28 node_ptr node = _link_dest( link );
29 node_ptr left = node->left;
30 node_ptr lright = left->right;
31
32 _link_set_dest( link, left );
33 left->parent = node->parent;
34
35 left->right = node;
36 node->parent = left;
37
38 node->left = lright;
39 if( lright )
40 lright->parent = node;
41 }
42
Now we move on to insertion.
The plan is to figure out where to insert the node, then to create a node and attach it, then to balance the tree. If the value already exists in the tree, we just don't insert it again.
To make things simpler, we'll have some of the complicated work put into separate functions. The code for the insert function is the following.
1 // Insert data into the tree
2 void insert( const_reference value )
3 {
4 // We need both the link and the parent
5 pair<link_type, node_ptr> where;
6 where = _get_insert_link( value );
7 if( ! where.first )
8 return;
9
10 // Create the node
11 node_ptr node = new rb_node;
12 node->data = value;
13 node->color = RED;
14 node->left = node->right = nullptr;
15 node->parent = where.second;
16
17 // Attach it to the tree
18 _link_set_dest( where.first, node );
19
20 // Balance
21 _insert_balance( node );
22 }
23
2 void insert( const_reference value )
3 {
4 // We need both the link and the parent
5 pair<link_type, node_ptr> where;
6 where = _get_insert_link( value );
7 if( ! where.first )
8 return;
9
10 // Create the node
11 node_ptr node = new rb_node;
12 node->data = value;
13 node->color = RED;
14 node->left = node->right = nullptr;
15 node->parent = where.second;
16
17 // Attach it to the tree
18 _link_set_dest( where.first, node );
19
20 // Balance
21 _insert_balance( node );
22 }
23
The _get_insert_link function returns a pair (if you're unfamiliar with std::pair, this means that it returns two things) with the first value being the link and the second being the origin of the link (the future parent of the node we're inserting). If the value already exists, then the link it returns is not valid, which can be tested with !where.first. We will need to include the utility header file to use std::pair.
The _link_set_dest function we have already covered. And the _insert_balance function just balances the tree after insertion. We pass the _insert_balance function the node we just created, since that's where we changed the tree and thus where we need to start balancing.
We set the node that we just inserted to red. While this isn't the only option that we have, it makes it easier if we can indeed insert a red node. Red nodes don't affect the black height, so if _insert_balance doesn't detect two reds in a row after this, then we don't even have to balance the tree. If we insert a black node, then we would more likely have to balance the tree afterwards.
The following is the code for the _get_insert_link function. We will cover the other undefined function, _insert_balance, in the next section. So, after this function is coded, we can move on to coding balancing.
1 /*
2 * Helper functions
3 */
4
5 // ...
6
7 // Figure out where to insert a value in the tree
8 // Returns a pair, where first is the link (nullptr if the
9 // value is already in the tree) and second is the origin
10 // of the link.
11 pair<link_type, node_ptr>
12 _get_insert_link( const_reference value )
13 {
14 link_type where = _make_link(_root);
15 node_ptr origin = nullptr;
16
17 while( _link_dest(where) ) {
18 origin = _link_dest(where);
19 if( value < origin->data )
20 where = _make_link( origin->left );
21 else if( value > origin->data )
22 where = _make_link( origin->right );
23 else {
24 where = nullptr;
25 break;
26 }
27 }
28
29 return make_pair( where, origin );
30 }
31
2 * Helper functions
3 */
4
5 // ...
6
7 // Figure out where to insert a value in the tree
8 // Returns a pair, where first is the link (nullptr if the
9 // value is already in the tree) and second is the origin
10 // of the link.
11 pair<link_type, node_ptr>
12 _get_insert_link( const_reference value )
13 {
14 link_type where = _make_link(_root);
15 node_ptr origin = nullptr;
16
17 while( _link_dest(where) ) {
18 origin = _link_dest(where);
19 if( value < origin->data )
20 where = _make_link( origin->left );
21 else if( value > origin->data )
22 where = _make_link( origin->right );
23 else {
24 where = nullptr;
25 break;
26 }
27 }
28
29 return make_pair( where, origin );
30 }
31
The _get_insert_link function works just like the find function, except that, instead of keeping track of the current node as it works its way down, it keeps track of the link to the current node and that node's parent (aka the link's origin).
Easy balancing after insertion.
Balancing after an insertion is a pain, so it may be a good time for a quick break before continuing. Ah, it's not near as bad as erasing, but it can get messy.
We will start with the easiest cases: one, we just inserted a red node and its parent is black; and two, we just inserted into an empty tree.
The picture on the left is if we insert a red node and the parent is black. Since we do follow the rules for red-black trees, we know that the parent of the red node was balanced before we inserted the node. Thus, the right child must be a null leaf or a red node. In any case, the total black height of that node was two, and each of its child subtrees had a black height of one.. After inserting the red node on the left, the total black height at the red node's parent is still two, and each of its child subtrees still have a black height of one. Therefore, inserting a red node with a black parent is a breeze! We need not balance.
The picture on the right is if we insert a node at the root. The only rule that we are violating is that the root must be black. Simply change the color to black, and we are done!
If neither of the two pictures above apply, then the red node that we just inserted has a red parent, and we need to take steps to fix the problem.
The far left is the situation that we have. We know that the parent has no other children since it must have been balanced before we inserted its child node. To solve the problem of two reds in a row, we can either change the node we just inserted to black (middle) or the parent to black (right).
I personally like the solution on the right. In either case, we are adding one to the black height and thus must go up the tree correcting the problem, but in the solution on the right, we can start balancing at the parent instead of at the node we just inserted. One step higher! It might make a difference in speed.
We will save the complicated "go up the tree fixing the black height problem" for a separate function. For the easy cases and for preparing to go up the tree balancing, this is our _insert_balance function:
1 /*
2 * Helper functions
3 */
4
5 // ...
6
7 // Balance the tree after insertion
8 // This function only handles the easy cases. The harder
9 // cases are handed off to another function.
10 void _insert_balance( node_ptr node )
11 {
12 // We just inserted at the root?
13 if( ! node->parent ) {
14 node->color = BLACK;
15 return; // done
16 }
17
18 // We just inserted a red as a black's child?
19 if( _node_color(node->parent) == BLACK )
20 return; // done
21
22 // Otherwise... we have two reds in a row
23 node->parent->color = BLACK;
24 _insert_harder_balancing( node->parent );
25 }
26
2 * Helper functions
3 */
4
5 // ...
6
7 // Balance the tree after insertion
8 // This function only handles the easy cases. The harder
9 // cases are handed off to another function.
10 void _insert_balance( node_ptr node )
11 {
12 // We just inserted at the root?
13 if( ! node->parent ) {
14 node->color = BLACK;
15 return; // done
16 }
17
18 // We just inserted a red as a black's child?
19 if( _node_color(node->parent) == BLACK )
20 return; // done
21
22 // Otherwise... we have two reds in a row
23 node->parent->color = BLACK;
24 _insert_harder_balancing( node->parent );
25 }
26
Harder recursing up the tree balancing after insertion.
There is no super simple way to solve this problem that I can think of, so we need to make it easier by taking it one step at a time. We need to consider every possibility that makes sense.
We will first consider the possibilities when first calling the _insert_harder_balancing function. Also, get your gedit, notepad, or whatever you use handy. If we run into a place where we need to traverse on up the tree, we need to make a note of any new possibilities that we introduce.
When first calling the function, the node we passed is black and its parent is black (node was red in _insert_balance before it was changed to black, so node's parent must be black). Let's look at this.
The red node with the yellow dot is the node that we just inserted. The blue numbers are the black heights at each node. The red node's parent is what we passed to our function (henceforth known as "node"). It used to have a black height of 1 since it used to be red, so its parent (henceforth known as "parent") used to have a black height of 2. If parent used to have a black height of 2 and is black, then node's sibling (henceforth, "sibling") has a black height of 1. The tree is unbalanced.
Since sibling has a black height of 1, then it is either red or a null leaf. This makes things much simpler! Let's look at these two possibilities.
Initial case 1: node is black, parent is black, sibling is red.
Since sibling has a black height of 1, if it is red, then it can only have null leaves as children. Now, how can we do color changes or rotations to solve the black imbalance at parent?
What if we set parent to red and sibling to black? That balances the tree (each side has a black height of 2), and the total black height is 2. As long as parent's parent is not red (it is either black or nonexistant (parent is root)), we're done! But if parent's parent is red, then we have a problem.
Well, the solution is to either set parent (um, the second red node from the left) to black or to set parent's parent (the top node) to black. In either case, we'll have to traverse up the tree balancing, but if we set parent's parent to black, then we can jump up the tree further before we balance.
Let's look at what the tree looks like after we jump on up the tree. node is now parent->parent, parent is its parent, and sibling is the new node's parent. It sounds confusing, but we actually don't have to worry about those details. Just call _insert_harder_balancing with parent->parent, and all those variables are adjusted accordingly exactly as they were when called initially. Let's have a picture of when we step upwards.
Since the old parent->parent (now "node") was red, then the new "parent" must be black. That makes the new "sibling" able to be pretty much anything! All that we know for certain is that it must have a height of at least 2 (since that's the minimum after calling from the initial call of _insert_harder_balancing), and so it must exist. But its children may be red, black, or null leaves (considered black by the _node_color function). That's five extra cases right there! We must make a note of these new possibilities.
Hopefully, we will inadvertently solve each of the cases listed above. If not, then I guess we'll just have to deal with them later. Let's continue with the initial cases for now.
Initial case 2: node is black, parent is black, sibling is null leaf.
Oh, thank god! I immediately see a way to not only balance this tree but to also get the total black height back to what it was before insertion. We need not traverse up the tree and consider other cases.
Reminder: The red node with the yellow dot is what we just inserted. node is its parent, and parent is node's parent.
To solve this, set parent to red, then rotate clockwise about parent. The picture below is the outcome of these operations.
There is one minor error in the above solution. I will leave it as an exercise to figure out what it is. If you can't figure it out, don't worry. I will correct the error at the end of the insertion section.
We are done with the easy insertion cases.
The code below is what we have so far for the _insert_harder_balancing function. The next step is to address those five extra cases we introduced, but first let's just look at the code we have for the initial cases.
1 /*
2 * Helper functions
3 */
4
5 // ...
6
7 // Balance the tree after insertion
8 // This function handles the harder cases.
9 void _insert_harder_balancing( node_ptr node )
10 {
11 node_ptr parent = node->parent;
12 node_ptr sibling = _node_sibling( node );
13
14 // Initial case 1: node black, par black, sib red
15 if( _node_color(sibling) == RED ) {
16 sibling->color = BLACK;
17 parent->color = RED;
18
19 // If parent's parent is red
20 if( _node_color(parent->parent) == RED ) {
21 parent->parent->color = BLACK;
22 _insert_harder_balancing( parent->parent );
23 }
24 }
25
26 // Initial case 1: node black, par black, sib null
27 else {
28 parent->color = RED;
29 _rotate_clockwise( _get_parent_link(parent) );
30 }
31 }
32
2 * Helper functions
3 */
4
5 // ...
6
7 // Balance the tree after insertion
8 // This function handles the harder cases.
9 void _insert_harder_balancing( node_ptr node )
10 {
11 node_ptr parent = node->parent;
12 node_ptr sibling = _node_sibling( node );
13
14 // Initial case 1: node black, par black, sib red
15 if( _node_color(sibling) == RED ) {
16 sibling->color = BLACK;
17 parent->color = RED;
18
19 // If parent's parent is red
20 if( _node_color(parent->parent) == RED ) {
21 parent->parent->color = BLACK;
22 _insert_harder_balancing( parent->parent );
23 }
24 }
25
26 // Initial case 1: node black, par black, sib null
27 else {
28 parent->color = RED;
29 _rotate_clockwise( _get_parent_link(parent) );
30 }
31 }
32
We also introduced the _node_sibling function. Nobody wants to see messy "get the sibling" code in an already complex function, so that code has its own function. The code for it is below.
1 /*
2 * Helper functions
3 */
4
5 // ...
6
7 // Get a node's sibling
8 node_ptr _node_sibling( node_ptr node )
9 {
10 node_ptr par = node->parent;
11 node_ptr sib = par->left;
12 if( sib == node )
13 sib = par->right;
14 return sib;
15 }
16
2 * Helper functions
3 */
4
5 // ...
6
7 // Get a node's sibling
8 node_ptr _node_sibling( node_ptr node )
9 {
10 node_ptr par = node->parent;
11 node_ptr sib = par->left;
12 if( sib == node )
13 sib = par->right;
14 return sib;
15 }
16
And it is time for those five more insertion cases.
Currently, our code will balance the five other cases without us having to do anything else. Remember that the null leaf nodes in case 2 can also be considered black. Let's look at what happens in each of the five extra cases. I have color-coded node, parent, and sibling so that you can follow what happens.
One question that you may ask is, "what if node's right child is red?". Well, looking at the code where we eventually get to this case, node was red before it was changed to black and the function was called again for these cases. If node was red, then its children must be black. No problems!
By the way, my punctuating after quotation marks is technically a grammar mistake, but I have no intention of changing it. So, for the quest for the grammatical error, keep, looking. :)
We are done with insertion!
It is time to view our _insert_harder_balancing function. Look below to find the code.
One thing to note, is that all of the examples above assume that node is on the left of its parent, and all of the drafts of _insert_harder_balancing make this assumption, too. If it is, instead, on its parent's right, then everything needs to be viewed in a mirror. In other words, where we rotate clockwise, we need to rotate counterclockwise.
1 // Balance the tree after insertion
2 // This function handles the harder cases.
3 void _insert_harder_balancing( node_ptr node )
4 {
5 node_ptr parent = node->parent;
6 node_ptr sibling = _node_sibling( node );
7
8 // Initial case 1: node black, par black, sib red
9 if( _node_color(sibling) == RED ) {
10 sibling->color = BLACK;
11 parent->color = RED;
12
13 // If parent's parent is red
14 if( _node_color(parent->parent) == RED ) {
15 parent->parent->color = BLACK;
16 _insert_harder_balancing( parent->parent );
17 }
18 }
19
20 // Initial case 2: node black, par black, sib black
21 else {
22 parent->color = RED;
23 if( node == parent->left ) {
24 _rotate_clockwise(
25 _get_parent_link(parent) );
26 }
27 else {
28 _rotate_counterclockwise(
29 _get_parent_link(parent) );
30 }
31 }
32 }
33
2 // This function handles the harder cases.
3 void _insert_harder_balancing( node_ptr node )
4 {
5 node_ptr parent = node->parent;
6 node_ptr sibling = _node_sibling( node );
7
8 // Initial case 1: node black, par black, sib red
9 if( _node_color(sibling) == RED ) {
10 sibling->color = BLACK;
11 parent->color = RED;
12
13 // If parent's parent is red
14 if( _node_color(parent->parent) == RED ) {
15 parent->parent->color = BLACK;
16 _insert_harder_balancing( parent->parent );
17 }
18 }
19
20 // Initial case 2: node black, par black, sib black
21 else {
22 parent->color = RED;
23 if( node == parent->left ) {
24 _rotate_clockwise(
25 _get_parent_link(parent) );
26 }
27 else {
28 _rotate_counterclockwise(
29 _get_parent_link(parent) );
30 }
31 }
32 }
33
And now, before we move on to erasing, let's run our program to make sure that everything works as planned... I'm compiling it... I'm running it... error! The root is red?
Why is the root red? Don't we set it to black if we just inserted at the root? Yes, we do. Looking further into it, in the _insert_harder_balancing function, we see that our case 1 handler might make the root red. For the cases above, we did not consider the rule about the root having to be black (to simplify things).
There are two solutions that we can choose from: one, add an extra "if" for case 1 that checks to see if parent is root before setting its color to red; or two: set the root to black after we return back to _insert_balance. The first solution will execute that "if" an unknown number of times, but the second solution will only execute the assignment once. Let's go with the second solution.
Let's try this again. Compiling... running... arg! Remember when I said that there was a problem with case 2? What if node's right child is red? We get two reds in a row after the rotation! The solution is to swap the colors of node and its right child, then rotate counterclockwise, if its right child is red. And no, this doesn't cause any more red violations after the rotation since node's right child's children must be black. An opposite method is used if node is on the right side of its parent.
One more try. Compiling... running... success! The code we have so far is below. It works wonderfully!
1 /*
2 * red-black tree example
3 * by Nathan Belue
4 * on April 19, 2011
5 *
6 * Feel free to do whatever you want with this code. If you
7 * choose to edit it, though, please either make a note of the
8 * edit or remove me as an author.
9 *
10 * Also, see my blog post on red-black trees at <http://nathanbelue.blogspot.com/2012/04/red-black-trees.html>
11 */
12
13
14 /*
15 * Included files
16 */
17
18 #include <cstdlib>
19 #include <iostream>
20 #include <utility>
21
22 using namespace std;
23
24
25
26 /*
27 * Some constants and typedefs
28 */
29
30 // The type of data to store
31 typedef int value_type;
32
33 // A constant reference to the type of data to store
34 typedef const value_type & const_reference;
35
36 // I really LOVE C++11's nullptr, but TR1 doesn't support it
37 #if __cplusplus < 201103L
38 #define nullptr 0
39 // ... so now it does
40 #endif
41
42
43
44 /*
45 * For representing colors
46 */
47
48 enum color_type
49 {
50 RED,
51 BLACK
52 };
53
54
55
56 /*
57 * Red-black tree node
58 */
59
60
61 // Our node struct
62 struct rb_node
63 {
64 value_type data;
65 color_type color;
66 rb_node * parent;
67 rb_node * left;
68 rb_node * right;
69 };
70
71 // I don't like typing out pointer types
72 typedef rb_node * node_ptr;
73
74
75
76 /*
77 * Red-black tree class
78 */
79
80 class rb_tree
81 {
82 /*
83 * Data
84 */
85
86 // The root of the tree
87 node_ptr _root;
88
89
90 /*
91 * Typedefs
92 */
93
94 // A link typedef
95 typedef node_ptr * link_type;
96
97
98 protected:
99
100
101 /*
102 * Helper functions
103 */
104
105
106 // A handy function for getting a node's color
107 // It even works for imaginary leaf nodes!
108 color_type _node_color( node_ptr node )
109 {
110 if( node )
111 return node->color;
112 return BLACK;
113 }
114
115 // Get a node's sibling
116 node_ptr _node_sibling( node_ptr node )
117 {
118 node_ptr par = node->parent;
119 node_ptr sib = par->left;
120 if( sib == node )
121 sib = par->right;
122 return sib;
123 }
124
125
126 // Convert a node pointer to a link
127 // You must pass it something like node->left.
128 // Passing it just node or just left won't work.
129 link_type _make_link( node_ptr & node )
130 {
131 return & node;
132 }
133
134 // Get a node's parent's link to that node
135 link_type _get_parent_link( node_ptr node )
136 {
137 node_ptr parent = node->parent;
138 if( ! parent )
139 return _make_link( _root );
140 if( parent->left == node )
141 return _make_link( parent->left );
142 //if( parent->right == node )
143 return _make_link( parent->right );
144 }
145
146 // Get a link's destination
147 node_ptr _link_dest( link_type link )
148 {
149 return *link;
150 }
151
152 // Set a link's destination
153 void _link_set_dest( link_type link, node_ptr dest )
154 {
155 *link = dest;
156 }
157
158 // Get a link's origin
159 node_ptr _link_orig( link_type link )
160 {
161 return _link_dest(link) -> parent;
162 }
163
164
165 // Clear out the data in a subtree
166 void _clear( node_ptr subtree )
167 {
168 if( subtree ) {
169 _clear( subtree->left );
170 _clear( subtree->right );
171 delete subtree;
172 }
173 }
174
175
176 // Rotate about a node counterclockwise
177 void _rotate_counterclockwise( link_type link )
178 {
179 node_ptr node = _link_dest(link);
180 node_ptr right = node->right;
181 node_ptr rleft = right->left;
182
183 _link_set_dest( link, right );
184 right->parent = node->parent;
185
186 right->left = node;
187 node->parent = right;
188
189 node->right = rleft;
190 if( rleft )
191 rleft->parent = node;
192 }
193
194 // Rotate about a node clockwise
195 void _rotate_clockwise( link_type link )
196 {
197 node_ptr node = _link_dest( link );
198 node_ptr left = node->left;
199 node_ptr lright = left->right;
200
201 _link_set_dest( link, left );
202 left->parent = node->parent;
203
204 left->right = node;
205 node->parent = left;
206
207 node->left = lright;
208 if( lright )
209 lright->parent = node;
210 }
211
212
213 // Figure out where to insert a value in the tree
214 // Returns a pair, where first is the link (nullptr if the
215 // value is already in the tree) and second is the origin
216 // of the link.
217 pair<link_type, node_ptr>
218 _get_insert_link( const_reference value )
219 {
220 link_type where = _make_link(_root);
221 node_ptr origin = nullptr;
222
223 while( _link_dest(where) ) {
224 origin = _link_dest(where);
225 if( value < origin->data )
226 where = _make_link( origin->left );
227 else if( value > origin->data )
228 where = _make_link( origin->right );
229 else {
230 where = nullptr;
231 break;
232 }
233 }
234
235 return make_pair( where, origin );
236 }
237
238
239 // Balance the tree after insertion
240 // This function handles the harder cases.
241 void _insert_harder_balancing( node_ptr node )
242 {
243 node_ptr parent = node->parent;
244 node_ptr sibling = _node_sibling( node );
245
246 // Initial case 1: node black, par black, sib red
247 if( _node_color(sibling) == RED ) {
248 sibling->color = BLACK;
249 parent->color = RED;
250
251 // If parent's parent is red
252 if( _node_color(parent->parent) == RED ) {
253 parent->parent->color = BLACK;
254 _insert_harder_balancing( parent->parent );
255 }
256 }
257
258 // Initial case 2: node black, par black, sib black
259 else {
260 parent->color = RED;
261 if( node == parent->left ) {
262 if( _node_color(node->right) == RED ) {
263 node->color = RED;
264 node->right->color = BLACK;
265 _rotate_counterclockwise(
266 _make_link(parent->left) );
267 }
268 _rotate_clockwise(
269 _get_parent_link(parent) );
270 }
271 else {
272 if( _node_color(node->left) == RED ) {
273 node->color = RED;
274 node->left->color = BLACK;
275 _rotate_clockwise(
276 _make_link(parent->right) );
277 }
278 _rotate_counterclockwise(
279 _get_parent_link(parent) );
280 }
281 }
282 }
283
284 // Balance the tree after insertion
285 // This function only handles the easy cases. The harder
286 // cases are handed off to another function.
287 void _insert_balance( node_ptr node )
288 {
289 // We just inserted at the root?
290 if( ! node->parent ) {
291 node->color = BLACK;
292 return; // done
293 }
294
295 // We just inserted a red as a black's child?
296 if( _node_color(node->parent) == BLACK )
297 return; // done
298
299 // Otherwise... we have two reds in a row
300 node->parent->color = BLACK;
301 _insert_harder_balancing( node->parent );
302 _root->color = BLACK;
303 }
304
305
306 // Check helper function
307 // Returns the black height of a subtree
308 int _check( node_ptr subtree )
309 {
310 // Imaginary leaf? black height is 1
311 if( ! subtree )
312 return 1;
313
314 node_ptr left = subtree->left;
315 node_ptr right = subtree->right;
316
317 // Black height of both sides must be the same
318 int left_height = _check( left );
319 int right_height = _check( right );
320 if( left_height != right_height )
321 throw "black imbalance!";
322
323 // No two reds in a row
324 if( _node_color(subtree) == RED ) {
325 if( _node_color(left) == RED
326 || _node_color(right) == RED )
327 throw "two reds in a row!";
328 }
329
330 // We're black, the height is [left|right]_height + 1
331 else
332 ++ left_height;
333
334 // Make sure that the children's parents are correct
335 if( left && left->parent != subtree
336 || right && right->parent != subtree )
337 throw "parent pointer wrong!";
338
339 // Return our height
340 return left_height;
341 }
342
343
344 public:
345
346 /*
347 * Interface functions
348 */
349
350
351 // Constructor
352 rb_tree() : _root(nullptr)
353 {
354 }
355
356
357 // Destructor
358 ~rb_tree()
359 {
360 _clear( _root );
361 }
362
363
364 // Clear out the data in the tree
365 void clear()
366 {
367 _clear( _root );
368 _root = nullptr;
369 }
370
371
372 // Find data in the tree
373 // Returns nullptr if not found; otherwise the node that
374 // contains the data.
375 node_ptr find( const_reference value )
376 {
377 node_ptr node = _root;
378 while( node ) {
379 if( value < node->data )
380 node = node->left;
381 else if( value > node->data )
382 node = node->right;
383 else
384 break;
385 }
386 return node;
387 }
388
389
390 // Insert data into the tree
391 void insert( const_reference value )
392 {
393 // We need both the link and the parent
394 pair<link_type, node_ptr> where;
395 where = _get_insert_link( value );
396 if( ! where.first )
397 return;
398
399 // Create the node
400 node_ptr node = new rb_node;
401 node->data = value;
402 node->color = RED;
403 node->left = node->right = nullptr;
404 node->parent = where.second;
405
406 // Attach it to the tree
407 _link_set_dest( where.first, node );
408
409 // Balance
410 _insert_balance( node );
411 }
412
413
414 // Erase data from the tree
415 void erase( const_reference value )
416 {
417 }
418
419
420 // Make sure that the tree is valid
421 // Throws an error if it isn't.
422 void check()
423 {
424 if( _node_color(_root) == RED )
425 throw "root is red!";
426
427 _check( _root );
428 }
429
430 };
431
432
433
434 /*
435 * Testing section
436 */
437
438
439 // Test insertion
440 // Fills the tree with a lot of random data
441 void test_insertion( rb_tree & tree, int count )
442 {
443 for( int i = 0; i != count; ++i ) {
444 int r = rand() % 3000;
445 tree.insert( r );
446 tree.check();
447 }
448 }
449
450
451 // Test erasing
452 // Erases random data from the tree
453 void test_erasing( rb_tree & tree, int count )
454 {
455 for( int i = 0; i != count; ++i ) {
456 int r = rand() % 3000;
457 tree.erase( r );
458 tree.check();
459 }
460 }
461
462
463 // Main function
464 int main()
465 {
466 try {
467 rb_tree tree;
468 test_insertion( tree, 1000 );
469 test_erasing( tree, 1000 );
470 }
471 catch( const char * e ) {
472 cerr << e << endl;
473 return 1;
474 }
475 }
476
2 * red-black tree example
3 * by Nathan Belue
4 * on April 19, 2011
5 *
6 * Feel free to do whatever you want with this code. If you
7 * choose to edit it, though, please either make a note of the
8 * edit or remove me as an author.
9 *
10 * Also, see my blog post on red-black trees at <http://nathanbelue.blogspot.com/2012/04/red-black-trees.html>
11 */
12
13
14 /*
15 * Included files
16 */
17
18 #include <cstdlib>
19 #include <iostream>
20 #include <utility>
21
22 using namespace std;
23
24
25
26 /*
27 * Some constants and typedefs
28 */
29
30 // The type of data to store
31 typedef int value_type;
32
33 // A constant reference to the type of data to store
34 typedef const value_type & const_reference;
35
36 // I really LOVE C++11's nullptr, but TR1 doesn't support it
37 #if __cplusplus < 201103L
38 #define nullptr 0
39 // ... so now it does
40 #endif
41
42
43
44 /*
45 * For representing colors
46 */
47
48 enum color_type
49 {
50 RED,
51 BLACK
52 };
53
54
55
56 /*
57 * Red-black tree node
58 */
59
60
61 // Our node struct
62 struct rb_node
63 {
64 value_type data;
65 color_type color;
66 rb_node * parent;
67 rb_node * left;
68 rb_node * right;
69 };
70
71 // I don't like typing out pointer types
72 typedef rb_node * node_ptr;
73
74
75
76 /*
77 * Red-black tree class
78 */
79
80 class rb_tree
81 {
82 /*
83 * Data
84 */
85
86 // The root of the tree
87 node_ptr _root;
88
89
90 /*
91 * Typedefs
92 */
93
94 // A link typedef
95 typedef node_ptr * link_type;
96
97
98 protected:
99
100
101 /*
102 * Helper functions
103 */
104
105
106 // A handy function for getting a node's color
107 // It even works for imaginary leaf nodes!
108 color_type _node_color( node_ptr node )
109 {
110 if( node )
111 return node->color;
112 return BLACK;
113 }
114
115 // Get a node's sibling
116 node_ptr _node_sibling( node_ptr node )
117 {
118 node_ptr par = node->parent;
119 node_ptr sib = par->left;
120 if( sib == node )
121 sib = par->right;
122 return sib;
123 }
124
125
126 // Convert a node pointer to a link
127 // You must pass it something like node->left.
128 // Passing it just node or just left won't work.
129 link_type _make_link( node_ptr & node )
130 {
131 return & node;
132 }
133
134 // Get a node's parent's link to that node
135 link_type _get_parent_link( node_ptr node )
136 {
137 node_ptr parent = node->parent;
138 if( ! parent )
139 return _make_link( _root );
140 if( parent->left == node )
141 return _make_link( parent->left );
142 //if( parent->right == node )
143 return _make_link( parent->right );
144 }
145
146 // Get a link's destination
147 node_ptr _link_dest( link_type link )
148 {
149 return *link;
150 }
151
152 // Set a link's destination
153 void _link_set_dest( link_type link, node_ptr dest )
154 {
155 *link = dest;
156 }
157
158 // Get a link's origin
159 node_ptr _link_orig( link_type link )
160 {
161 return _link_dest(link) -> parent;
162 }
163
164
165 // Clear out the data in a subtree
166 void _clear( node_ptr subtree )
167 {
168 if( subtree ) {
169 _clear( subtree->left );
170 _clear( subtree->right );
171 delete subtree;
172 }
173 }
174
175
176 // Rotate about a node counterclockwise
177 void _rotate_counterclockwise( link_type link )
178 {
179 node_ptr node = _link_dest(link);
180 node_ptr right = node->right;
181 node_ptr rleft = right->left;
182
183 _link_set_dest( link, right );
184 right->parent = node->parent;
185
186 right->left = node;
187 node->parent = right;
188
189 node->right = rleft;
190 if( rleft )
191 rleft->parent = node;
192 }
193
194 // Rotate about a node clockwise
195 void _rotate_clockwise( link_type link )
196 {
197 node_ptr node = _link_dest( link );
198 node_ptr left = node->left;
199 node_ptr lright = left->right;
200
201 _link_set_dest( link, left );
202 left->parent = node->parent;
203
204 left->right = node;
205 node->parent = left;
206
207 node->left = lright;
208 if( lright )
209 lright->parent = node;
210 }
211
212
213 // Figure out where to insert a value in the tree
214 // Returns a pair, where first is the link (nullptr if the
215 // value is already in the tree) and second is the origin
216 // of the link.
217 pair<link_type, node_ptr>
218 _get_insert_link( const_reference value )
219 {
220 link_type where = _make_link(_root);
221 node_ptr origin = nullptr;
222
223 while( _link_dest(where) ) {
224 origin = _link_dest(where);
225 if( value < origin->data )
226 where = _make_link( origin->left );
227 else if( value > origin->data )
228 where = _make_link( origin->right );
229 else {
230 where = nullptr;
231 break;
232 }
233 }
234
235 return make_pair( where, origin );
236 }
237
238
239 // Balance the tree after insertion
240 // This function handles the harder cases.
241 void _insert_harder_balancing( node_ptr node )
242 {
243 node_ptr parent = node->parent;
244 node_ptr sibling = _node_sibling( node );
245
246 // Initial case 1: node black, par black, sib red
247 if( _node_color(sibling) == RED ) {
248 sibling->color = BLACK;
249 parent->color = RED;
250
251 // If parent's parent is red
252 if( _node_color(parent->parent) == RED ) {
253 parent->parent->color = BLACK;
254 _insert_harder_balancing( parent->parent );
255 }
256 }
257
258 // Initial case 2: node black, par black, sib black
259 else {
260 parent->color = RED;
261 if( node == parent->left ) {
262 if( _node_color(node->right) == RED ) {
263 node->color = RED;
264 node->right->color = BLACK;
265 _rotate_counterclockwise(
266 _make_link(parent->left) );
267 }
268 _rotate_clockwise(
269 _get_parent_link(parent) );
270 }
271 else {
272 if( _node_color(node->left) == RED ) {
273 node->color = RED;
274 node->left->color = BLACK;
275 _rotate_clockwise(
276 _make_link(parent->right) );
277 }
278 _rotate_counterclockwise(
279 _get_parent_link(parent) );
280 }
281 }
282 }
283
284 // Balance the tree after insertion
285 // This function only handles the easy cases. The harder
286 // cases are handed off to another function.
287 void _insert_balance( node_ptr node )
288 {
289 // We just inserted at the root?
290 if( ! node->parent ) {
291 node->color = BLACK;
292 return; // done
293 }
294
295 // We just inserted a red as a black's child?
296 if( _node_color(node->parent) == BLACK )
297 return; // done
298
299 // Otherwise... we have two reds in a row
300 node->parent->color = BLACK;
301 _insert_harder_balancing( node->parent );
302 _root->color = BLACK;
303 }
304
305
306 // Check helper function
307 // Returns the black height of a subtree
308 int _check( node_ptr subtree )
309 {
310 // Imaginary leaf? black height is 1
311 if( ! subtree )
312 return 1;
313
314 node_ptr left = subtree->left;
315 node_ptr right = subtree->right;
316
317 // Black height of both sides must be the same
318 int left_height = _check( left );
319 int right_height = _check( right );
320 if( left_height != right_height )
321 throw "black imbalance!";
322
323 // No two reds in a row
324 if( _node_color(subtree) == RED ) {
325 if( _node_color(left) == RED
326 || _node_color(right) == RED )
327 throw "two reds in a row!";
328 }
329
330 // We're black, the height is [left|right]_height + 1
331 else
332 ++ left_height;
333
334 // Make sure that the children's parents are correct
335 if( left && left->parent != subtree
336 || right && right->parent != subtree )
337 throw "parent pointer wrong!";
338
339 // Return our height
340 return left_height;
341 }
342
343
344 public:
345
346 /*
347 * Interface functions
348 */
349
350
351 // Constructor
352 rb_tree() : _root(nullptr)
353 {
354 }
355
356
357 // Destructor
358 ~rb_tree()
359 {
360 _clear( _root );
361 }
362
363
364 // Clear out the data in the tree
365 void clear()
366 {
367 _clear( _root );
368 _root = nullptr;
369 }
370
371
372 // Find data in the tree
373 // Returns nullptr if not found; otherwise the node that
374 // contains the data.
375 node_ptr find( const_reference value )
376 {
377 node_ptr node = _root;
378 while( node ) {
379 if( value < node->data )
380 node = node->left;
381 else if( value > node->data )
382 node = node->right;
383 else
384 break;
385 }
386 return node;
387 }
388
389
390 // Insert data into the tree
391 void insert( const_reference value )
392 {
393 // We need both the link and the parent
394 pair<link_type, node_ptr> where;
395 where = _get_insert_link( value );
396 if( ! where.first )
397 return;
398
399 // Create the node
400 node_ptr node = new rb_node;
401 node->data = value;
402 node->color = RED;
403 node->left = node->right = nullptr;
404 node->parent = where.second;
405
406 // Attach it to the tree
407 _link_set_dest( where.first, node );
408
409 // Balance
410 _insert_balance( node );
411 }
412
413
414 // Erase data from the tree
415 void erase( const_reference value )
416 {
417 }
418
419
420 // Make sure that the tree is valid
421 // Throws an error if it isn't.
422 void check()
423 {
424 if( _node_color(_root) == RED )
425 throw "root is red!";
426
427 _check( _root );
428 }
429
430 };
431
432
433
434 /*
435 * Testing section
436 */
437
438
439 // Test insertion
440 // Fills the tree with a lot of random data
441 void test_insertion( rb_tree & tree, int count )
442 {
443 for( int i = 0; i != count; ++i ) {
444 int r = rand() % 3000;
445 tree.insert( r );
446 tree.check();
447 }
448 }
449
450
451 // Test erasing
452 // Erases random data from the tree
453 void test_erasing( rb_tree & tree, int count )
454 {
455 for( int i = 0; i != count; ++i ) {
456 int r = rand() % 3000;
457 tree.erase( r );
458 tree.check();
459 }
460 }
461
462
463 // Main function
464 int main()
465 {
466 try {
467 rb_tree tree;
468 test_insertion( tree, 1000 );
469 test_erasing( tree, 1000 );
470 }
471 catch( const char * e ) {
472 cerr << e << endl;
473 return 1;
474 }
475 }
476
Erasing
To erase from a red-black tree, you first erase just like you do for a regular binary search tree, then you balance the tree and make sure it follows the rules for a red-black tree. If you don't remember or know how to erase from a regular binary search tree, no worries! I will go into more detail on that now. Consider the binary search tree below.
When you erase a node, there are four possibilities: 1) the node is the only node in the tree; 2) the node has no children; 3) the node has one child; 4) the node has two children.
In the first case, where you erase the only node in the tree, just erase it! In the second case, it's the same thing. You erase a node with no children, and everything is still dandy (apart from balancing afterwards for the second case).
In the third case, things get a little tricky. In the tree above, what happens if you just delete 8? Well, the root of the tree no longer has a path to 5, 6, or 7! This is, however, easy to fix. Just move the 6 up to where 8 is after you delete it. Oh, and notice that the values will still be in alphabetical order (left to right), too.
In the fourth case, what do you do? What if you want to delete 2? "Oh, just move the 3 up!" Yea, that works for that instance. Now what about 4? You can't just move the 8 up to take its place. Go ahead, try it. Neither can you move the 2 up to take its place. How can you remove the 4 from the tree? And here, it gets slightly tricky, but there is a solution!
If a node that you want to remove from the tree has two children, swap its value with either the rightmost node of its left subtree or the leftmost node of its right subtree. Either of those two will have at most one child. Then, use the case for no children or one child to remove the replacement node. Here, look (I'll use the leftmost node of the right subtree):
Notice that the values are still in alphabetical order after the 4 is swapped with the 5 and the 4 is removed.
We will use the solutions above to code a _replace_and_remove_node function that will help us out in erasing. What it will do is make the tree forget that the node ever existed. If it has one child, the node will be replaced by its child. If it has two children, the leftmost node of its right subtree will replace it. If it has no children, then it will be simply forgotten.
Since we are wanting to balance the tree after the modifications, we will make _replace_and_remove_node return the actual removed node (remember, we don't actually remove the node we wanted to remove if it has two children). What returning this will do is tell us where the tree was modified, and we will use this information to figure out where to start balancing. Since we will not delete the node yet, it still has its outgoing pointer to its parent (though its parent has forgotten it).
The code for the _replace_and_remove_node function is below. After this is done, we can more easily code the main erase function.
1 /*
2 * Helper functions
3 */
4
5 // ...
6
7 // Return the leftmost node of a subtree
8 node_ptr _node_leftmost( node_ptr node )
9 {
10 while( node->left )
11 node = node->left;
12 return node;
13 }
14
15 // ...
16
17 // [Possibly] replace and remove a node
18 // Returns the actual node removed from the tree
19 node_ptr _replace_and_remove_node( node_ptr node )
20 {
21 node_ptr rep = nullptr;
22
23 if( node->left && node->right ) {
24 rep = _node_leftmost( node->right );
25 std::swap( rep->data, node->data );
26 node = rep;
27 rep = nullptr;
28 }
29
30 if( node->left )
31 rep = node->left;
32 else if( node->right )
33 rep = node->right;
34
35 _link_set_dest( _get_parent_link(node), rep );
36 if( rep )
37 rep->parent = node->parent;
38
39 return node;
40 }
41
2 * Helper functions
3 */
4
5 // ...
6
7 // Return the leftmost node of a subtree
8 node_ptr _node_leftmost( node_ptr node )
9 {
10 while( node->left )
11 node = node->left;
12 return node;
13 }
14
15 // ...
16
17 // [Possibly] replace and remove a node
18 // Returns the actual node removed from the tree
19 node_ptr _replace_and_remove_node( node_ptr node )
20 {
21 node_ptr rep = nullptr;
22
23 if( node->left && node->right ) {
24 rep = _node_leftmost( node->right );
25 std::swap( rep->data, node->data );
26 node = rep;
27 rep = nullptr;
28 }
29
30 if( node->left )
31 rep = node->left;
32 else if( node->right )
33 rep = node->right;
34
35 _link_set_dest( _get_parent_link(node), rep );
36 if( rep )
37 rep->parent = node->parent;
38
39 return node;
40 }
41
Notice we also added a _node_leftmost helper function. And now the part of erasing that remove a node from the tree is finished! Now we can move on to erasing.
To erase a value, we need to find the node that contains the value. After we find that node, we remove it from the tree, balance the tree, then delete the node. Here is the code:
1 // Erase data from the tree
2 void erase( const_reference value )
3 {
4 node_ptr node = find( value );
5 if( ! node )
6 return;
7
8 node = _replace_and_remove_node( node );
9
10 _erase_balance( node );
11
12 delete node;
13 }
14
2 void erase( const_reference value )
3 {
4 node_ptr node = find( value );
5 if( ! node )
6 return;
7
8 node = _replace_and_remove_node( node );
9
10 _erase_balance( node );
11
12 delete node;
13 }
14
We passed the removed not to the balance function. We might want to know what color the node we removed was. Remember that the node still exists and still has a link to its parent (though its parent no longer has a link to it). And now we can begin the complicated task of balancing after a deletion.
Easy Balancing for Erasing
First, we will start with the easy cases, as we did for insertion. If we can not solve the problem easily, we will call another function for the more complicated cases.
Remember that we must make sure that the tree follows the red-black tree rules. To make things simpler, we will only be concerned with the rules that two reds cannot be in a row and every path from a node to a decendant leaf must contain the same number of black nodes.
When we erase a node, it has at most one child (as is ensured after the call to _replace_and_remove_node). Also, it can be either red or black. Consider the picture below.
Continuing with our current color scheme, the blue is the black height at a node, the green lines are the links between the nodes, and the circles are the nodes (red and black). One added symbol is the yellow X which covers the node that we have removed from the tree.
The bottom-right situation is impossible because the tree is unbalanced before the removal of the red node. The other three cases, though, are possible. In the top-left case, we have no choice but to consider even more nodes, and we will do this in a different function. The case on the right can be solved right away by making the red node black. The bottom-left case has no effect on the black height of the tree, so we need not balance in that case.
See? In the second and third situation, the black height is the same as it was before, so we are okay. It is only in the first situation that we have a problem.
On more thing to consider, however, is what to do if we just removed the root. The first and second cases above could also represent that, so we will have the balancing down. In the first case, why pass the work on to another function that handles complicated stuff, though, when we can just return without balancing if we just deleted the root? We will do that.
1 // Balance the tree after erasing
2 // Node is the node that was removed
3 void _erase_balance( node_ptr node )
4 {
5 // If we just deleted a red node, we're done
6 if( _node_color(node) == RED )
7 return;
8
9 // If we deleted a black node, but it has a red child
10 if( node->left || node->right ) {
11 if( node->left )
12 node->left->color = BLACK;
13 else
14 node->right->color = BLACK;
15 return;
16 }
17
18 // If we just deleted the root, we're done
19 if( ! node->parent )
20 return;
21
22 // Otherwise, we have a black node with no children
23 _erase_harder_balancing( ??? );
24 }
25
2 // Node is the node that was removed
3 void _erase_balance( node_ptr node )
4 {
5 // If we just deleted a red node, we're done
6 if( _node_color(node) == RED )
7 return;
8
9 // If we deleted a black node, but it has a red child
10 if( node->left || node->right ) {
11 if( node->left )
12 node->left->color = BLACK;
13 else
14 node->right->color = BLACK;
15 return;
16 }
17
18 // If we just deleted the root, we're done
19 if( ! node->parent )
20 return;
21
22 // Otherwise, we have a black node with no children
23 _erase_harder_balancing( ??? );
24 }
25
We took a shortcut for the black node with a red child. If we just removed a black node, we must have a red child if there is any child. Also, we used _node_color to get the node's color. As explained way up above, _node_color works even for those imaginary leaf nodes, but we use it for everything just to stay consistent.
I put question marks after the _erase_harder_balancing function, which handles the first case in the picture above. Where should we start considering the harder cases?
Well, we know that the node is black and has no children, so do we need to pass the node? Not really. But we do need to know which side of the subtree now has one less black node, so we do need to pass this information somehow. Well, we can't pass node because its parent no longer knows it. Let's pass its sibling. This way, we know which side is heavier, and we can start balancing at the parent. But what if the sibling doesn't exist? It must, because if it didn't exist, the black height of the side we removed from was 2 and its sibling's side was 1, which would have been unbalanced. We can and shall pass the removed node's sibling.
1 // Balance the tree after erasing
2 // Node is the node that was removed
3 void _erase_balance( node_ptr node )
4 {
5 // If we just deleted a red node, we're done
6 if( _node_color(node) == RED )
7 return;
8
9 // If we deleted a black node, but it has a red child
10 if( node->left || node->right ) {
11 if( node->left )
12 node->left->color = BLACK;
13 else
14 node->right->color = BLACK;
15 return;
16 }
17
18 // If we just deleted the root, we're done
19 if( ! node->parent )
20 return;
21
22 // Otherwise, we have a black node with no children
23 node_ptr sib = node->parent->left;
24 if( ! sib )
25 sib = node->parent->right;
26 _erase_harder_balancing( sib );
27 }
28
2 // Node is the node that was removed
3 void _erase_balance( node_ptr node )
4 {
5 // If we just deleted a red node, we're done
6 if( _node_color(node) == RED )
7 return;
8
9 // If we deleted a black node, but it has a red child
10 if( node->left || node->right ) {
11 if( node->left )
12 node->left->color = BLACK;
13 else
14 node->right->color = BLACK;
15 return;
16 }
17
18 // If we just deleted the root, we're done
19 if( ! node->parent )
20 return;
21
22 // Otherwise, we have a black node with no children
23 node_ptr sib = node->parent->left;
24 if( ! sib )
25 sib = node->parent->right;
26 _erase_harder_balancing( sib );
27 }
28
We can't use the _node_sibling function since the parent no longer recognizes the removed node, but we know that the removed node has no child and was replaced with nullptr, and we can use that to figure out the sibling (the sibling is the only side of parent that exists).
Now let's consider more difficult initial cases for erasing.
First, we will consider the initial cases. What does the tree look like right after we remove a node when we have gone to _erase_harder_balancing?
By looking at just the colors of the sibling and the parent, I cannot find a solution. All of the solutions I can think of depend on either the color of sibling's left child or the colors of both of its children.
We need to expand these cases to cover sibling's children. Since we are considering every possible combination of the colors of the parent, the sibling, and the children of sibling, we may as well just throw out the idea of only considering the simpler initial cases. Now we have the possibilities listed below.
Since null nodes are considered black, the above works also for the initial cases where sibling's children may be null. Also, we will still assume that node is black, but if we have traversed up the tree, it will exist (so I've left off the yellow X). We just have to make sure that node is black when we traverse up the tree.
One last thing to note about the picture is that I used "h" as a variable to hold the height of the parent. The other nodes have a height relative to this. This is because the height may be any number as we traverse up the tree.
Now we find solutions for the cases where erasing.
Our goal is to change colors and/or do rotations so that the total black height of the subtree is the same as it was before and the subtree is balanced. Sometimes, we can't get the height to be the same as it was before. In such a case, we need to traverse on up the tree.
One more thing to consider is whether we have made the root of the subtree red while its parent's color is red. We may have a problem if we have. We will need to fix that problem and then traverse on up the tree.
Now let us begin the tedious task of finding solutions to each of the nine cases. I hope you are fully rested and have a while to dedicate to this! It might get hard. Oh, and I'll skip the transitions from case to solution and leave those as practice for you. It will be good to work these out so that you understand the process better.
I will use P to represent parent, S to represent sibling, Sl to represent sibling's left child, and Sr to represent sibling's right child. I'll do this to make the typing in the case titles less. I will likely use the full names in the instructions, though.
Case 1: P is black, S is black, Sl is black, Sr is black
In this case, we can simply set the sibling's color to red. That fixes the black height problem. Unfortunately, the total height of the tree is now one less than it was before.
We will need to traverse on up the tree balancing. Since our _erase_harder_balancing function takes the sibling of the node that is on the smaller side of the tree as a parameter, we pass parent's sibling to _erase_harder_balancing to traverse upwards.
Case 2: P is black, S is black, Sl is red, Sr is black
In this case, set sibling's left child to black, rotate clockwise about sibling, then rotate counterclockwise about parent. Check it out!
I color-coded the nodes so that you could follow them. I did not show each step — that is an exercise for you! And we are done for this case.
Case 3: P is black, S is black, Sl is black, Sr is red
In this case, simply set the sibling's right child to black and then rotate counterclockwise about parent. Then, we are done!
Case 4: P is black, S is black, Sl is red, Sr is red
The solution here is to do exactly as in case 2. Set sibling's left child to black, rotate clockwise about sibling, then rotate counterclockwise about parent. Then, we are done.
Case 5: P is black, S is red, Sl is black, Sr is black
While I am thinking about it, let me point out that setting node to red would solve the problem completely if we just consider the part of the subtree shown in case 5. The reason we cannot do this is that we do not know that node's children are not red. We just came from there, too, so we do not want to backtrack to check node's children.
Now, back to case 5... I cannot find a solution from what is shown. The closest that I can come is the picture shown below, but the left side has an imbalance afterwards. I set parent to red and sibling to black, then I rotate counterclockwise about parent.
Isn't it ironic how we must traverse back down the tree right after I said not to? We must traverse back down the tree and pass the green-centered node to our _erase_harder_balancing function (remember, we pass the sibling of the node that has lost one black height).
We don't want to parse through cases 1, 2, 3, 4, and 6 when all we need to do is parse through cases 6, 7, 8, and 9 for this. Why not put 6, 7, 8, and 9 in a separate function? We will do that!
Case 6: P is red, S is black, Sl is black, Sr is black
In this case, we can simply rotate counterclockwise about parent. I won't color-code the nodes since it's so simple. Oh, and we're done afterwards!
Case 7: P is red, S is black, Sl is red, Sr is black
In this case, set parent to black, rotate clockwise at sibling, then rotate counterclockwise at parent. Then, we are done.
Case 8: P is red, S is black, Sl is black, Sr is red
The solution here is the same as in case 6. Just rotate counterclockwise about parent! Since it's so simple, no color-coding. And we are done afterwards since the total black height before is the total black height afterwards.
Case 9: P is red, S is black, Sl is red, Sr is red
Set parent to black, rotate clockwise about sibling, then rotate counterclockwise about parent. Total height is what it was before, so we need not traverse on up the tree. We are done.
Case one more: we are at the root
If we have just balanced the tree and the new subtree's root is the root of the entire tree, then we cannot traverse upwards. Therefore, we need to check to make sure that parent->parent exists every time we want to traverse upwards. Problem solved!
Now that the cases and solutions are discovered, code it!
All of the cases that we considered above assume that the node (which is the side that is low one black height) is on the left of its parent. If it is on the right, then just hold the solution up to a mirror.
We could use extra if statements to determine which side of its parent that node is on, but that makes the code messier. Instead, I will use a little trick that turns the rotations around and swaps the variables we use for the sibling's children.
1 // Use default rotations and sib->left|right
2 typedef void (rb_tree::*rot_func)( link_type );
3 rot_func rot_clock = & rb_tree::_rotate_clockwise;
4 rot_func rot_counter= & rb_tree::_rotate_counterclockwise;
5 node_ptr sib_left = sibling->left;
6 node_ptr sib_right = sibling->right;
7
8 // But if sibling is on the left, turn them around.
9 if( sibling == sibling->parent->left ) {
10 swap( rot_clock, rot_counter );
11 swap( sib_left, sib_right );
12 }
13
2 typedef void (rb_tree::*rot_func)( link_type );
3 rot_func rot_clock = & rb_tree::_rotate_clockwise;
4 rot_func rot_counter= & rb_tree::_rotate_counterclockwise;
5 node_ptr sib_left = sibling->left;
6 node_ptr sib_right = sibling->right;
7
8 // But if sibling is on the left, turn them around.
9 if( sibling == sibling->parent->left ) {
10 swap( rot_clock, rot_counter );
11 swap( sib_left, sib_right );
12 }
13
Now we just look at each case and its solution above and code it as we see it. Don't worry about optimization. We just want to make a tree that works! Later, we can optimize (not covered in this tutorial). The code below is the _erase_harder_balancing function.
1 // Harder balancing stuff
2 void _erase_harder_balancing( node_ptr sibling )
3 {
4 // Use default rotations and sib->left|right
5 typedef void (rb_tree::*rot_func)( link_type );
6 rot_func rot_clock = & rb_tree::_rotate_clockwise;
7 rot_func rot_counter= & rb_tree::_rotate_counterclockwise;
8 node_ptr sib_left = sibling->left;
9 node_ptr sib_right = sibling->right;
10
11 // But if sibling is on the left, turn them around.
12 if( sibling == sibling->parent->left ) {
13 swap( rot_clock, rot_counter );
14 swap( sib_left, sib_right );
15 }
16
17 // One more variable
18 node_ptr parent = sibling->parent;
19
20 // Case 1-5: parent is black
21 if( _node_color(parent) == BLACK ) {
22
23 // Case 1-4: sibling is black
24 if( _node_color(sibling) == BLACK ) {
25
26 // Case 1: sibling's children are both black
27 if( _node_color(sib_left) == BLACK
28 && _node_color(sib_right) == BLACK ) {
29 sibling->color = RED;
30 if( parent->parent ) {
31 _erase_harder_balancing(
32 _node_sibling(parent) );
33 }
34 }
35
36 // Case 2: sib_left is red, sib_right is black
37 else if( _node_color(sib_left) == RED
38 && _node_color(sib_right) == BLACK ) {
39 sib_left->color = BLACK;
40 (this->*rot_clock)(
41 _get_parent_link(sibling) );
42 (this->*rot_counter)(
43 _get_parent_link(parent) );
44 }
45
46 // Case 3: sib_left is black, sib_right is red
47 else if( _node_color(sib_left) == BLACK
48 && _node_color(sib_right) == RED ) {
49 sib_right->color = BLACK;
50 (this->*rot_counter)(
51 _get_parent_link(parent) );
52 }
53
54 // Case 4: sibling's children are both red
55 else {
56 sib_left->color = BLACK;
57 (this->*rot_clock)(
58 _get_parent_link(sibling) );
59 (this->*rot_counter)(
60 _get_parent_link(parent) );
61 }
62
63 }
64
65 // Case 5: sibling is red
66 else {
67 parent->color = RED;
68 sibling->color = BLACK;
69 (this->*rot_counter)( _get_parent_link(parent) );
70 _erase_harder_balancing_red_parent( sib_left );
71 }
72
73 }
74
75 // Case 6-9: parent is red
76 else {
77 _erase_harder_balancing_red_parent( sibling );
78 }
79 }
80
2 void _erase_harder_balancing( node_ptr sibling )
3 {
4 // Use default rotations and sib->left|right
5 typedef void (rb_tree::*rot_func)( link_type );
6 rot_func rot_clock = & rb_tree::_rotate_clockwise;
7 rot_func rot_counter= & rb_tree::_rotate_counterclockwise;
8 node_ptr sib_left = sibling->left;
9 node_ptr sib_right = sibling->right;
10
11 // But if sibling is on the left, turn them around.
12 if( sibling == sibling->parent->left ) {
13 swap( rot_clock, rot_counter );
14 swap( sib_left, sib_right );
15 }
16
17 // One more variable
18 node_ptr parent = sibling->parent;
19
20 // Case 1-5: parent is black
21 if( _node_color(parent) == BLACK ) {
22
23 // Case 1-4: sibling is black
24 if( _node_color(sibling) == BLACK ) {
25
26 // Case 1: sibling's children are both black
27 if( _node_color(sib_left) == BLACK
28 && _node_color(sib_right) == BLACK ) {
29 sibling->color = RED;
30 if( parent->parent ) {
31 _erase_harder_balancing(
32 _node_sibling(parent) );
33 }
34 }
35
36 // Case 2: sib_left is red, sib_right is black
37 else if( _node_color(sib_left) == RED
38 && _node_color(sib_right) == BLACK ) {
39 sib_left->color = BLACK;
40 (this->*rot_clock)(
41 _get_parent_link(sibling) );
42 (this->*rot_counter)(
43 _get_parent_link(parent) );
44 }
45
46 // Case 3: sib_left is black, sib_right is red
47 else if( _node_color(sib_left) == BLACK
48 && _node_color(sib_right) == RED ) {
49 sib_right->color = BLACK;
50 (this->*rot_counter)(
51 _get_parent_link(parent) );
52 }
53
54 // Case 4: sibling's children are both red
55 else {
56 sib_left->color = BLACK;
57 (this->*rot_clock)(
58 _get_parent_link(sibling) );
59 (this->*rot_counter)(
60 _get_parent_link(parent) );
61 }
62
63 }
64
65 // Case 5: sibling is red
66 else {
67 parent->color = RED;
68 sibling->color = BLACK;
69 (this->*rot_counter)( _get_parent_link(parent) );
70 _erase_harder_balancing_red_parent( sib_left );
71 }
72
73 }
74
75 // Case 6-9: parent is red
76 else {
77 _erase_harder_balancing_red_parent( sibling );
78 }
79 }
80
And the following is the code for _erase_harder_balancing_red_parent. Remember, we separated it out because of case 5. Okay, so we have optimized a little already, haha...
1 // Harder balancing stuff
2 // Handles cases where parent is red
3 void _erase_harder_balancing_red_parent( node_ptr sibling )
4 {
5 // Use default rotations and sib->left|right
6 typedef void (rb_tree::*rot_func)( link_type );
7 rot_func rot_clock = & rb_tree::_rotate_clockwise;
8 rot_func rot_counter= & rb_tree::_rotate_counterclockwise;
9 node_ptr sib_left = sibling->left;
10 node_ptr sib_right = sibling->right;
11
12 // But if sibling is on the left, turn them around.
13 if( sibling == sibling->parent->left ) {
14 swap( rot_clock, rot_counter );
15 swap( sib_left, sib_right );
16 }
17
18 // One more variable
19 node_ptr parent = sibling->parent;
20
21 // Parent is red, by the way
22 // Sibling must be black.
23
24 // Case 6: both of sibling's children are black
25 if( _node_color(sib_left) == BLACK
26 && _node_color(sib_right) == BLACK ) {
27 (this->*rot_counter)( _get_parent_link(parent) );
28 }
29
30 // Case 7: sib_left is red, sib_right is black
31 else if( _node_color(sib_left) == RED
32 && _node_color(sib_right) == BLACK ) {
33 parent->color = BLACK;
34 (this->*rot_clock)( _get_parent_link(sibling) );
35 (this->*rot_counter)( _get_parent_link(parent) );
36 }
37
38 // Case 8: sib_left is black, sib_right is red
39 else if( _node_color(sib_left) == BLACK
40 && _node_color(sib_right) == RED ) {
41 (this->*rot_counter)( _get_parent_link(parent) );
42 }
43
44 // Case 9: both of sibling's children are red
45 else {
46 parent->color = BLACK;
47 (this->*rot_clock)( _get_parent_link(sibling) );
48 (this->*rot_counter)( _get_parent_link(parent) );
49 }
50 }
51
2 // Handles cases where parent is red
3 void _erase_harder_balancing_red_parent( node_ptr sibling )
4 {
5 // Use default rotations and sib->left|right
6 typedef void (rb_tree::*rot_func)( link_type );
7 rot_func rot_clock = & rb_tree::_rotate_clockwise;
8 rot_func rot_counter= & rb_tree::_rotate_counterclockwise;
9 node_ptr sib_left = sibling->left;
10 node_ptr sib_right = sibling->right;
11
12 // But if sibling is on the left, turn them around.
13 if( sibling == sibling->parent->left ) {
14 swap( rot_clock, rot_counter );
15 swap( sib_left, sib_right );
16 }
17
18 // One more variable
19 node_ptr parent = sibling->parent;
20
21 // Parent is red, by the way
22 // Sibling must be black.
23
24 // Case 6: both of sibling's children are black
25 if( _node_color(sib_left) == BLACK
26 && _node_color(sib_right) == BLACK ) {
27 (this->*rot_counter)( _get_parent_link(parent) );
28 }
29
30 // Case 7: sib_left is red, sib_right is black
31 else if( _node_color(sib_left) == RED
32 && _node_color(sib_right) == BLACK ) {
33 parent->color = BLACK;
34 (this->*rot_clock)( _get_parent_link(sibling) );
35 (this->*rot_counter)( _get_parent_link(parent) );
36 }
37
38 // Case 8: sib_left is black, sib_right is red
39 else if( _node_color(sib_left) == BLACK
40 && _node_color(sib_right) == RED ) {
41 (this->*rot_counter)( _get_parent_link(parent) );
42 }
43
44 // Case 9: both of sibling's children are red
45 else {
46 parent->color = BLACK;
47 (this->*rot_clock)( _get_parent_link(sibling) );
48 (this->*rot_counter)( _get_parent_link(parent) );
49 }
50 }
51
We are finished!
Test the code. Compiling... running... success! And now, hopefully, you have a better grasp of red-black trees. At the very least, you now have some red-black tree code! Feel free to use it however you see fit. Oh, and you don't even have to give me credit (though a +1 would be nice). ;) Oh, and the code for the entire thing is below.
1 /*
2 * red-black tree example
3 * by Nathan Belue
4 * on April 19, 2011
5 *
6 * Feel free to do whatever you want with this code. If you
7 * choose to edit it, though, please either make a note of the
8 * edit or remove me as an author.
9 *
10 * Also, see my blog post on red-black trees at <http://nathanbelue.blogspot.com/2012/04/red-black-trees.html>
11 */
12
13
14 /*
15 * Included files
16 */
17
18 #include <cstdlib>
19 #include <iostream>
20 #include <utility>
21
22 using namespace std;
23
24
25
26 /*
27 * Some constants and typedefs
28 */
29
30 // The type of data to store
31 typedef int value_type;
32
33 // A constant reference to the type of data to store
34 typedef const value_type & const_reference;
35
36 // I really LOVE C++11's nullptr, but TR1 doesn't support it
37 #if __cplusplus < 201103L
38 #define nullptr 0
39 // ... so now it does
40 #endif
41
42
43
44 /*
45 * For representing colors
46 */
47
48 enum color_type
49 {
50 RED,
51 BLACK
52 };
53
54
55
56 /*
57 * Red-black tree node
58 */
59
60
61 // Our node struct
62 struct rb_node
63 {
64 value_type data;
65 color_type color;
66 rb_node * parent;
67 rb_node * left;
68 rb_node * right;
69 };
70
71 // I don't like typing out pointer types
72 typedef rb_node * node_ptr;
73
74
75
76 /*
77 * Red-black tree class
78 */
79
80 class rb_tree
81 {
82 /*
83 * Data
84 */
85
86 // The root of the tree
87 node_ptr _root;
88
89
90 /*
91 * Typedefs
92 */
93
94 // A link typedef
95 typedef node_ptr * link_type;
96
97
98 protected:
99
100
101 /*
102 * Helper functions
103 */
104
105
106 // A handy function for getting a node's color
107 // It even works for imaginary leaf nodes!
108 color_type _node_color( node_ptr node )
109 {
110 if( node )
111 return node->color;
112 return BLACK;
113 }
114
115 // Get a node's sibling
116 node_ptr _node_sibling( node_ptr node )
117 {
118 node_ptr par = node->parent;
119 node_ptr sib = par->left;
120 if( sib == node )
121 sib = par->right;
122 return sib;
123 }
124
125 // Return the leftmost node of a subtree
126 node_ptr _node_leftmost( node_ptr node )
127 {
128 while( node->left )
129 node = node->left;
130 return node;
131 }
132
133
134 // Convert a node pointer to a link
135 // You must pass it something like node->left.
136 // Passing it just node or just left won't work.
137 link_type _make_link( node_ptr & node )
138 {
139 return & node;
140 }
141
142 // Get a node's parent's link to that node
143 link_type _get_parent_link( node_ptr node )
144 {
145 node_ptr parent = node->parent;
146 if( ! parent )
147 return _make_link( _root );
148 if( parent->left == node )
149 return _make_link( parent->left );
150 //if( parent->right == node )
151 return _make_link( parent->right );
152 }
153
154 // Get a link's destination
155 node_ptr _link_dest( link_type link )
156 {
157 return *link;
158 }
159
160 // Set a link's destination
161 void _link_set_dest( link_type link, node_ptr dest )
162 {
163 *link = dest;
164 }
165
166 // Get a link's origin
167 node_ptr _link_orig( link_type link )
168 {
169 return _link_dest(link) -> parent;
170 }
171
172
173 // Clear out the data in a subtree
174 void _clear( node_ptr subtree )
175 {
176 if( subtree ) {
177 _clear( subtree->left );
178 _clear( subtree->right );
179 delete subtree;
180 }
181 }
182
183
184 // Rotate about a node counterclockwise
185 void _rotate_counterclockwise( link_type link )
186 {
187 node_ptr node = _link_dest(link);
188 node_ptr right = node->right;
189 node_ptr rleft = right->left;
190
191 _link_set_dest( link, right );
192 right->parent = node->parent;
193
194 right->left = node;
195 node->parent = right;
196
197 node->right = rleft;
198 if( rleft )
199 rleft->parent = node;
200 }
201
202 // Rotate about a node clockwise
203 void _rotate_clockwise( link_type link )
204 {
205 node_ptr node = _link_dest( link );
206 node_ptr left = node->left;
207 node_ptr lright = left->right;
208
209 _link_set_dest( link, left );
210 left->parent = node->parent;
211
212 left->right = node;
213 node->parent = left;
214
215 node->left = lright;
216 if( lright )
217 lright->parent = node;
218 }
219
220
221 // Figure out where to insert a value in the tree
222 // Returns a pair, where first is the link (nullptr if the
223 // value is already in the tree) and second is the origin
224 // of the link.
225 pair<link_type, node_ptr>
226 _get_insert_link( const_reference value )
227 {
228 link_type where = _make_link(_root);
229 node_ptr origin = nullptr;
230
231 while( _link_dest(where) ) {
232 origin = _link_dest(where);
233 if( value < origin->data )
234 where = _make_link( origin->left );
235 else if( value > origin->data )
236 where = _make_link( origin->right );
237 else {
238 where = nullptr;
239 break;
240 }
241 }
242
243 return make_pair( where, origin );
244 }
245
246
247 // Balance the tree after insertion
248 // This function handles the harder cases.
249 void _insert_harder_balancing( node_ptr node )
250 {
251 node_ptr parent = node->parent;
252 node_ptr sibling = _node_sibling( node );
253
254 // Initial case 1: node black, par black, sib red
255 if( _node_color(sibling) == RED ) {
256 sibling->color = BLACK;
257 parent->color = RED;
258
259 // If parent's parent is red
260 if( _node_color(parent->parent) == RED ) {
261 parent->parent->color = BLACK;
262 _insert_harder_balancing( parent->parent );
263 }
264 }
265
266 // Initial case 2: node black, par black, sib black
267 else {
268 parent->color = RED;
269 if( node == parent->left ) {
270 if( _node_color(node->right) == RED ) {
271 node->color = RED;
272 node->right->color = BLACK;
273 _rotate_counterclockwise(
274 _make_link(parent->left) );
275 }
276 _rotate_clockwise(
277 _get_parent_link(parent) );
278 }
279 else {
280 if( _node_color(node->left) == RED ) {
281 node->color = RED;
282 node->left->color = BLACK;
283 _rotate_clockwise(
284 _make_link(parent->right) );
285 }
286 _rotate_counterclockwise(
287 _get_parent_link(parent) );
288 }
289 }
290 }
291
292 // Balance the tree after insertion
293 // This function only handles the easy cases. The harder
294 // cases are handed off to another function.
295 void _insert_balance( node_ptr node )
296 {
297 // We just inserted at the root?
298 if( ! node->parent ) {
299 node->color = BLACK;
300 return; // done
301 }
302
303 // We just inserted a red as a black's child?
304 if( _node_color(node->parent) == BLACK )
305 return; // done
306
307 // Otherwise... we have two reds in a row
308 node->parent->color = BLACK;
309 _insert_harder_balancing( node->parent );
310 _root->color = BLACK;
311 }
312
313
314 // [Possibly] replace and remove a node
315 // Returns the actual node removed from the tree
316 node_ptr _replace_and_remove_node( node_ptr node )
317 {
318 node_ptr rep = nullptr;
319
320 if( node->left && node->right ) {
321 rep = _node_leftmost( node->right );
322 std::swap( rep->data, node->data );
323 node = rep;
324 rep = nullptr;
325 }
326
327 if( node->left )
328 rep = node->left;
329 else if( node->right )
330 rep = node->right;
331
332 _link_set_dest( _get_parent_link(node), rep );
333 if( rep )
334 rep->parent = node->parent;
335
336 return node;
337 }
338
339 // Harder balancing stuff
340 // Handles cases where parent is red
341 void _erase_harder_balancing_red_parent( node_ptr sibling )
342 {
343 // Use default rotations and sib->left|right
344 typedef void (rb_tree::*rot_func)( link_type );
345 rot_func rot_clock = & rb_tree::_rotate_clockwise;
346 rot_func rot_counter= & rb_tree::_rotate_counterclockwise;
347 node_ptr sib_left = sibling->left;
348 node_ptr sib_right = sibling->right;
349
350 // But if sibling is on the left, turn them around.
351 if( sibling == sibling->parent->left ) {
352 swap( rot_clock, rot_counter );
353 swap( sib_left, sib_right );
354 }
355
356 // One more variable
357 node_ptr parent = sibling->parent;
358
359 // Parent is red, by the way
360 // Sibling must be black.
361
362 // Case 6: both of sibling's children are black
363 if( _node_color(sib_left) == BLACK
364 && _node_color(sib_right) == BLACK ) {
365 (this->*rot_counter)( _get_parent_link(parent) );
366 }
367
368 // Case 7: sib_left is red, sib_right is black
369 else if( _node_color(sib_left) == RED
370 && _node_color(sib_right) == BLACK ) {
371 parent->color = BLACK;
372 (this->*rot_clock)( _get_parent_link(sibling) );
373 (this->*rot_counter)( _get_parent_link(parent) );
374 }
375
376 // Case 8: sib_left is black, sib_right is red
377 else if( _node_color(sib_left) == BLACK
378 && _node_color(sib_right) == RED ) {
379 (this->*rot_counter)( _get_parent_link(parent) );
380 }
381
382 // Case 9: both of sibling's children are red
383 else {
384 parent->color = BLACK;
385 (this->*rot_clock)( _get_parent_link(sibling) );
386 (this->*rot_counter)( _get_parent_link(parent) );
387 }
388 }
389
390 // Harder balancing stuff
391 void _erase_harder_balancing( node_ptr sibling )
392 {
393 // Use default rotations and sib->left|right
394 typedef void (rb_tree::*rot_func)( link_type );
395 rot_func rot_clock = & rb_tree::_rotate_clockwise;
396 rot_func rot_counter= & rb_tree::_rotate_counterclockwise;
397 node_ptr sib_left = sibling->left;
398 node_ptr sib_right = sibling->right;
399
400 // But if sibling is on the left, turn them around.
401 if( sibling == sibling->parent->left ) {
402 swap( rot_clock, rot_counter );
403 swap( sib_left, sib_right );
404 }
405
406 // One more variable
407 node_ptr parent = sibling->parent;
408
409 // Case 1-5: parent is black
410 if( _node_color(parent) == BLACK ) {
411
412 // Case 1-4: sibling is black
413 if( _node_color(sibling) == BLACK ) {
414
415 // Case 1: sibling's children are both black
416 if( _node_color(sib_left) == BLACK
417 && _node_color(sib_right) == BLACK ) {
418 sibling->color = RED;
419 if( parent->parent ) {
420 _erase_harder_balancing(
421 _node_sibling(parent) );
422 }
423 }
424
425 // Case 2: sib_left is red, sib_right is black
426 else if( _node_color(sib_left) == RED
427 && _node_color(sib_right) == BLACK ) {
428 sib_left->color = BLACK;
429 (this->*rot_clock)(
430 _get_parent_link(sibling) );
431 (this->*rot_counter)(
432 _get_parent_link(parent) );
433 }
434
435 // Case 3: sib_left is black, sib_right is red
436 else if( _node_color(sib_left) == BLACK
437 && _node_color(sib_right) == RED ) {
438 sib_right->color = BLACK;
439 (this->*rot_counter)(
440 _get_parent_link(parent) );
441 }
442
443 // Case 4: sibling's children are both red
444 else {
445 sib_left->color = BLACK;
446 (this->*rot_clock)(
447 _get_parent_link(sibling) );
448 (this->*rot_counter)(
449 _get_parent_link(parent) );
450 }
451
452 }
453
454 // Case 5: sibling is red
455 else {
456 parent->color = RED;
457 sibling->color = BLACK;
458 (this->*rot_counter)( _get_parent_link(parent) );
459 _erase_harder_balancing_red_parent( sib_left );
460 }
461
462 }
463
464 // Case 6-9: parent is red
465 else {
466 _erase_harder_balancing_red_parent( sibling );
467 }
468 }
469
470 // Balance the tree after erasing
471 // Node is the node that was removed
472 void _erase_balance( node_ptr node )
473 {
474 // If we just deleted a red node, we're done
475 if( _node_color(node) == RED )
476 return;
477
478 // If we deleted a black node, but it has a red child
479 if( node->left || node->right ) {
480 if( node->left )
481 node->left->color = BLACK;
482 else
483 node->right->color = BLACK;
484 return;
485 }
486
487 // If we just deleted the root, we're done
488 if( ! node->parent )
489 return;
490
491 // Otherwise, we have a black node with no children
492 node_ptr sib = node->parent->left;
493 if( ! sib )
494 sib = node->parent->right;
495 _erase_harder_balancing( sib );
496 }
497
498
499 // Check helper function
500 // Returns the black height of a subtree
501 int _check( node_ptr subtree )
502 {
503 // Imaginary leaf? black height is 1
504 if( ! subtree )
505 return 1;
506
507 node_ptr left = subtree->left;
508 node_ptr right = subtree->right;
509
510 // Black height of both sides must be the same
511 int left_height = _check( left );
512 int right_height = _check( right );
513 if( left_height != right_height )
514 throw "black imbalance!";
515
516 // No two reds in a row
517 if( _node_color(subtree) == RED ) {
518 if( _node_color(left) == RED
519 || _node_color(right) == RED )
520 throw "two reds in a row!";
521 }
522
523 // We're black, the height is [left|right]_height + 1
524 else
525 ++ left_height;
526
527 // Make sure that the children's parents are correct
528 if( left && left->parent != subtree
529 || right && right->parent != subtree )
530 throw "parent pointer wrong!";
531
532 // Return our height
533 return left_height;
534 }
535
536
537 public:
538
539 /*
540 * Interface functions
541 */
542
543
544 // Constructor
545 rb_tree() : _root(nullptr)
546 {
547 }
548
549
550 // Destructor
551 ~rb_tree()
552 {
553 _clear( _root );
554 }
555
556
557 // Clear out the data in the tree
558 void clear()
559 {
560 _clear( _root );
561 _root = nullptr;
562 }
563
564
565 // Find data in the tree
566 // Returns nullptr if not found; otherwise the node that
567 // contains the data.
568 node_ptr find( const_reference value )
569 {
570 node_ptr node = _root;
571 while( node ) {
572 if( value < node->data )
573 node = node->left;
574 else if( value > node->data )
575 node = node->right;
576 else
577 break;
578 }
579 return node;
580 }
581
582
583 // Insert data into the tree
584 void insert( const_reference value )
585 {
586 // We need both the link and the parent
587 pair<link_type, node_ptr> where;
588 where = _get_insert_link( value );
589 if( ! where.first )
590 return;
591
592 // Create the node
593 node_ptr node = new rb_node;
594 node->data = value;
595 node->color = RED;
596 node->left = node->right = nullptr;
597 node->parent = where.second;
598
599 // Attach it to the tree
600 _link_set_dest( where.first, node );
601
602 // Balance
603 _insert_balance( node );
604 }
605
606
607 // Erase data from the tree
608 void erase( const_reference value )
609 {
610 node_ptr node = find( value );
611 if( ! node )
612 return;
613
614 node = _replace_and_remove_node( node );
615
616 _erase_balance( node );
617
618 delete node;
619 }
620
621
622 // Make sure that the tree is valid
623 // Throws an error if it isn't.
624 void check()
625 {
626 if( _node_color(_root) == RED )
627 throw "root is red!";
628
629 _check( _root );
630 }
631
632 };
633
634
635
636 /*
637 * Testing section
638 */
639
640
641 // Test insertion
642 // Fills the tree with a lot of random data
643 void test_insertion( rb_tree & tree, int count )
644 {
645 for( int i = 0; i != count; ++i ) {
646 int r = rand() % 3000;
647 tree.insert( r );
648 tree.check();
649 }
650 }
651
652
653 // Test erasing
654 // Erases random data from the tree
655 void test_erasing( rb_tree & tree, int count )
656 {
657 for( int i = 0; i != count; ++i ) {
658 int r = rand() % 3000;
659 tree.erase( r );
660 tree.check();
661 }
662 }
663
664
665 // Main function
666 int main()
667 {
668 try {
669 rb_tree tree;
670 test_insertion( tree, 1000 );
671 test_erasing( tree, 1000 );
672 }
673 catch( const char * e ) {
674 cerr << e << endl;
675 return 1;
676 }
677 }
678
2 * red-black tree example
3 * by Nathan Belue
4 * on April 19, 2011
5 *
6 * Feel free to do whatever you want with this code. If you
7 * choose to edit it, though, please either make a note of the
8 * edit or remove me as an author.
9 *
10 * Also, see my blog post on red-black trees at <http://nathanbelue.blogspot.com/2012/04/red-black-trees.html>
11 */
12
13
14 /*
15 * Included files
16 */
17
18 #include <cstdlib>
19 #include <iostream>
20 #include <utility>
21
22 using namespace std;
23
24
25
26 /*
27 * Some constants and typedefs
28 */
29
30 // The type of data to store
31 typedef int value_type;
32
33 // A constant reference to the type of data to store
34 typedef const value_type & const_reference;
35
36 // I really LOVE C++11's nullptr, but TR1 doesn't support it
37 #if __cplusplus < 201103L
38 #define nullptr 0
39 // ... so now it does
40 #endif
41
42
43
44 /*
45 * For representing colors
46 */
47
48 enum color_type
49 {
50 RED,
51 BLACK
52 };
53
54
55
56 /*
57 * Red-black tree node
58 */
59
60
61 // Our node struct
62 struct rb_node
63 {
64 value_type data;
65 color_type color;
66 rb_node * parent;
67 rb_node * left;
68 rb_node * right;
69 };
70
71 // I don't like typing out pointer types
72 typedef rb_node * node_ptr;
73
74
75
76 /*
77 * Red-black tree class
78 */
79
80 class rb_tree
81 {
82 /*
83 * Data
84 */
85
86 // The root of the tree
87 node_ptr _root;
88
89
90 /*
91 * Typedefs
92 */
93
94 // A link typedef
95 typedef node_ptr * link_type;
96
97
98 protected:
99
100
101 /*
102 * Helper functions
103 */
104
105
106 // A handy function for getting a node's color
107 // It even works for imaginary leaf nodes!
108 color_type _node_color( node_ptr node )
109 {
110 if( node )
111 return node->color;
112 return BLACK;
113 }
114
115 // Get a node's sibling
116 node_ptr _node_sibling( node_ptr node )
117 {
118 node_ptr par = node->parent;
119 node_ptr sib = par->left;
120 if( sib == node )
121 sib = par->right;
122 return sib;
123 }
124
125 // Return the leftmost node of a subtree
126 node_ptr _node_leftmost( node_ptr node )
127 {
128 while( node->left )
129 node = node->left;
130 return node;
131 }
132
133
134 // Convert a node pointer to a link
135 // You must pass it something like node->left.
136 // Passing it just node or just left won't work.
137 link_type _make_link( node_ptr & node )
138 {
139 return & node;
140 }
141
142 // Get a node's parent's link to that node
143 link_type _get_parent_link( node_ptr node )
144 {
145 node_ptr parent = node->parent;
146 if( ! parent )
147 return _make_link( _root );
148 if( parent->left == node )
149 return _make_link( parent->left );
150 //if( parent->right == node )
151 return _make_link( parent->right );
152 }
153
154 // Get a link's destination
155 node_ptr _link_dest( link_type link )
156 {
157 return *link;
158 }
159
160 // Set a link's destination
161 void _link_set_dest( link_type link, node_ptr dest )
162 {
163 *link = dest;
164 }
165
166 // Get a link's origin
167 node_ptr _link_orig( link_type link )
168 {
169 return _link_dest(link) -> parent;
170 }
171
172
173 // Clear out the data in a subtree
174 void _clear( node_ptr subtree )
175 {
176 if( subtree ) {
177 _clear( subtree->left );
178 _clear( subtree->right );
179 delete subtree;
180 }
181 }
182
183
184 // Rotate about a node counterclockwise
185 void _rotate_counterclockwise( link_type link )
186 {
187 node_ptr node = _link_dest(link);
188 node_ptr right = node->right;
189 node_ptr rleft = right->left;
190
191 _link_set_dest( link, right );
192 right->parent = node->parent;
193
194 right->left = node;
195 node->parent = right;
196
197 node->right = rleft;
198 if( rleft )
199 rleft->parent = node;
200 }
201
202 // Rotate about a node clockwise
203 void _rotate_clockwise( link_type link )
204 {
205 node_ptr node = _link_dest( link );
206 node_ptr left = node->left;
207 node_ptr lright = left->right;
208
209 _link_set_dest( link, left );
210 left->parent = node->parent;
211
212 left->right = node;
213 node->parent = left;
214
215 node->left = lright;
216 if( lright )
217 lright->parent = node;
218 }
219
220
221 // Figure out where to insert a value in the tree
222 // Returns a pair, where first is the link (nullptr if the
223 // value is already in the tree) and second is the origin
224 // of the link.
225 pair<link_type, node_ptr>
226 _get_insert_link( const_reference value )
227 {
228 link_type where = _make_link(_root);
229 node_ptr origin = nullptr;
230
231 while( _link_dest(where) ) {
232 origin = _link_dest(where);
233 if( value < origin->data )
234 where = _make_link( origin->left );
235 else if( value > origin->data )
236 where = _make_link( origin->right );
237 else {
238 where = nullptr;
239 break;
240 }
241 }
242
243 return make_pair( where, origin );
244 }
245
246
247 // Balance the tree after insertion
248 // This function handles the harder cases.
249 void _insert_harder_balancing( node_ptr node )
250 {
251 node_ptr parent = node->parent;
252 node_ptr sibling = _node_sibling( node );
253
254 // Initial case 1: node black, par black, sib red
255 if( _node_color(sibling) == RED ) {
256 sibling->color = BLACK;
257 parent->color = RED;
258
259 // If parent's parent is red
260 if( _node_color(parent->parent) == RED ) {
261 parent->parent->color = BLACK;
262 _insert_harder_balancing( parent->parent );
263 }
264 }
265
266 // Initial case 2: node black, par black, sib black
267 else {
268 parent->color = RED;
269 if( node == parent->left ) {
270 if( _node_color(node->right) == RED ) {
271 node->color = RED;
272 node->right->color = BLACK;
273 _rotate_counterclockwise(
274 _make_link(parent->left) );
275 }
276 _rotate_clockwise(
277 _get_parent_link(parent) );
278 }
279 else {
280 if( _node_color(node->left) == RED ) {
281 node->color = RED;
282 node->left->color = BLACK;
283 _rotate_clockwise(
284 _make_link(parent->right) );
285 }
286 _rotate_counterclockwise(
287 _get_parent_link(parent) );
288 }
289 }
290 }
291
292 // Balance the tree after insertion
293 // This function only handles the easy cases. The harder
294 // cases are handed off to another function.
295 void _insert_balance( node_ptr node )
296 {
297 // We just inserted at the root?
298 if( ! node->parent ) {
299 node->color = BLACK;
300 return; // done
301 }
302
303 // We just inserted a red as a black's child?
304 if( _node_color(node->parent) == BLACK )
305 return; // done
306
307 // Otherwise... we have two reds in a row
308 node->parent->color = BLACK;
309 _insert_harder_balancing( node->parent );
310 _root->color = BLACK;
311 }
312
313
314 // [Possibly] replace and remove a node
315 // Returns the actual node removed from the tree
316 node_ptr _replace_and_remove_node( node_ptr node )
317 {
318 node_ptr rep = nullptr;
319
320 if( node->left && node->right ) {
321 rep = _node_leftmost( node->right );
322 std::swap( rep->data, node->data );
323 node = rep;
324 rep = nullptr;
325 }
326
327 if( node->left )
328 rep = node->left;
329 else if( node->right )
330 rep = node->right;
331
332 _link_set_dest( _get_parent_link(node), rep );
333 if( rep )
334 rep->parent = node->parent;
335
336 return node;
337 }
338
339 // Harder balancing stuff
340 // Handles cases where parent is red
341 void _erase_harder_balancing_red_parent( node_ptr sibling )
342 {
343 // Use default rotations and sib->left|right
344 typedef void (rb_tree::*rot_func)( link_type );
345 rot_func rot_clock = & rb_tree::_rotate_clockwise;
346 rot_func rot_counter= & rb_tree::_rotate_counterclockwise;
347 node_ptr sib_left = sibling->left;
348 node_ptr sib_right = sibling->right;
349
350 // But if sibling is on the left, turn them around.
351 if( sibling == sibling->parent->left ) {
352 swap( rot_clock, rot_counter );
353 swap( sib_left, sib_right );
354 }
355
356 // One more variable
357 node_ptr parent = sibling->parent;
358
359 // Parent is red, by the way
360 // Sibling must be black.
361
362 // Case 6: both of sibling's children are black
363 if( _node_color(sib_left) == BLACK
364 && _node_color(sib_right) == BLACK ) {
365 (this->*rot_counter)( _get_parent_link(parent) );
366 }
367
368 // Case 7: sib_left is red, sib_right is black
369 else if( _node_color(sib_left) == RED
370 && _node_color(sib_right) == BLACK ) {
371 parent->color = BLACK;
372 (this->*rot_clock)( _get_parent_link(sibling) );
373 (this->*rot_counter)( _get_parent_link(parent) );
374 }
375
376 // Case 8: sib_left is black, sib_right is red
377 else if( _node_color(sib_left) == BLACK
378 && _node_color(sib_right) == RED ) {
379 (this->*rot_counter)( _get_parent_link(parent) );
380 }
381
382 // Case 9: both of sibling's children are red
383 else {
384 parent->color = BLACK;
385 (this->*rot_clock)( _get_parent_link(sibling) );
386 (this->*rot_counter)( _get_parent_link(parent) );
387 }
388 }
389
390 // Harder balancing stuff
391 void _erase_harder_balancing( node_ptr sibling )
392 {
393 // Use default rotations and sib->left|right
394 typedef void (rb_tree::*rot_func)( link_type );
395 rot_func rot_clock = & rb_tree::_rotate_clockwise;
396 rot_func rot_counter= & rb_tree::_rotate_counterclockwise;
397 node_ptr sib_left = sibling->left;
398 node_ptr sib_right = sibling->right;
399
400 // But if sibling is on the left, turn them around.
401 if( sibling == sibling->parent->left ) {
402 swap( rot_clock, rot_counter );
403 swap( sib_left, sib_right );
404 }
405
406 // One more variable
407 node_ptr parent = sibling->parent;
408
409 // Case 1-5: parent is black
410 if( _node_color(parent) == BLACK ) {
411
412 // Case 1-4: sibling is black
413 if( _node_color(sibling) == BLACK ) {
414
415 // Case 1: sibling's children are both black
416 if( _node_color(sib_left) == BLACK
417 && _node_color(sib_right) == BLACK ) {
418 sibling->color = RED;
419 if( parent->parent ) {
420 _erase_harder_balancing(
421 _node_sibling(parent) );
422 }
423 }
424
425 // Case 2: sib_left is red, sib_right is black
426 else if( _node_color(sib_left) == RED
427 && _node_color(sib_right) == BLACK ) {
428 sib_left->color = BLACK;
429 (this->*rot_clock)(
430 _get_parent_link(sibling) );
431 (this->*rot_counter)(
432 _get_parent_link(parent) );
433 }
434
435 // Case 3: sib_left is black, sib_right is red
436 else if( _node_color(sib_left) == BLACK
437 && _node_color(sib_right) == RED ) {
438 sib_right->color = BLACK;
439 (this->*rot_counter)(
440 _get_parent_link(parent) );
441 }
442
443 // Case 4: sibling's children are both red
444 else {
445 sib_left->color = BLACK;
446 (this->*rot_clock)(
447 _get_parent_link(sibling) );
448 (this->*rot_counter)(
449 _get_parent_link(parent) );
450 }
451
452 }
453
454 // Case 5: sibling is red
455 else {
456 parent->color = RED;
457 sibling->color = BLACK;
458 (this->*rot_counter)( _get_parent_link(parent) );
459 _erase_harder_balancing_red_parent( sib_left );
460 }
461
462 }
463
464 // Case 6-9: parent is red
465 else {
466 _erase_harder_balancing_red_parent( sibling );
467 }
468 }
469
470 // Balance the tree after erasing
471 // Node is the node that was removed
472 void _erase_balance( node_ptr node )
473 {
474 // If we just deleted a red node, we're done
475 if( _node_color(node) == RED )
476 return;
477
478 // If we deleted a black node, but it has a red child
479 if( node->left || node->right ) {
480 if( node->left )
481 node->left->color = BLACK;
482 else
483 node->right->color = BLACK;
484 return;
485 }
486
487 // If we just deleted the root, we're done
488 if( ! node->parent )
489 return;
490
491 // Otherwise, we have a black node with no children
492 node_ptr sib = node->parent->left;
493 if( ! sib )
494 sib = node->parent->right;
495 _erase_harder_balancing( sib );
496 }
497
498
499 // Check helper function
500 // Returns the black height of a subtree
501 int _check( node_ptr subtree )
502 {
503 // Imaginary leaf? black height is 1
504 if( ! subtree )
505 return 1;
506
507 node_ptr left = subtree->left;
508 node_ptr right = subtree->right;
509
510 // Black height of both sides must be the same
511 int left_height = _check( left );
512 int right_height = _check( right );
513 if( left_height != right_height )
514 throw "black imbalance!";
515
516 // No two reds in a row
517 if( _node_color(subtree) == RED ) {
518 if( _node_color(left) == RED
519 || _node_color(right) == RED )
520 throw "two reds in a row!";
521 }
522
523 // We're black, the height is [left|right]_height + 1
524 else
525 ++ left_height;
526
527 // Make sure that the children's parents are correct
528 if( left && left->parent != subtree
529 || right && right->parent != subtree )
530 throw "parent pointer wrong!";
531
532 // Return our height
533 return left_height;
534 }
535
536
537 public:
538
539 /*
540 * Interface functions
541 */
542
543
544 // Constructor
545 rb_tree() : _root(nullptr)
546 {
547 }
548
549
550 // Destructor
551 ~rb_tree()
552 {
553 _clear( _root );
554 }
555
556
557 // Clear out the data in the tree
558 void clear()
559 {
560 _clear( _root );
561 _root = nullptr;
562 }
563
564
565 // Find data in the tree
566 // Returns nullptr if not found; otherwise the node that
567 // contains the data.
568 node_ptr find( const_reference value )
569 {
570 node_ptr node = _root;
571 while( node ) {
572 if( value < node->data )
573 node = node->left;
574 else if( value > node->data )
575 node = node->right;
576 else
577 break;
578 }
579 return node;
580 }
581
582
583 // Insert data into the tree
584 void insert( const_reference value )
585 {
586 // We need both the link and the parent
587 pair<link_type, node_ptr> where;
588 where = _get_insert_link( value );
589 if( ! where.first )
590 return;
591
592 // Create the node
593 node_ptr node = new rb_node;
594 node->data = value;
595 node->color = RED;
596 node->left = node->right = nullptr;
597 node->parent = where.second;
598
599 // Attach it to the tree
600 _link_set_dest( where.first, node );
601
602 // Balance
603 _insert_balance( node );
604 }
605
606
607 // Erase data from the tree
608 void erase( const_reference value )
609 {
610 node_ptr node = find( value );
611 if( ! node )
612 return;
613
614 node = _replace_and_remove_node( node );
615
616 _erase_balance( node );
617
618 delete node;
619 }
620
621
622 // Make sure that the tree is valid
623 // Throws an error if it isn't.
624 void check()
625 {
626 if( _node_color(_root) == RED )
627 throw "root is red!";
628
629 _check( _root );
630 }
631
632 };
633
634
635
636 /*
637 * Testing section
638 */
639
640
641 // Test insertion
642 // Fills the tree with a lot of random data
643 void test_insertion( rb_tree & tree, int count )
644 {
645 for( int i = 0; i != count; ++i ) {
646 int r = rand() % 3000;
647 tree.insert( r );
648 tree.check();
649 }
650 }
651
652
653 // Test erasing
654 // Erases random data from the tree
655 void test_erasing( rb_tree & tree, int count )
656 {
657 for( int i = 0; i != count; ++i ) {
658 int r = rand() % 3000;
659 tree.erase( r );
660 tree.check();
661 }
662 }
663
664
665 // Main function
666 int main()
667 {
668 try {
669 rb_tree tree;
670 test_insertion( tree, 1000 );
671 test_erasing( tree, 1000 );
672 }
673 catch( const char * e ) {
674 cerr << e << endl;
675 return 1;
676 }
677 }
678
Footnotes and references:
1. Wikipedia, Red-Black Tree. <http://en.wikipedia.org/wiki/Red%E2%80%93black_tree>. 18 April 2012.

















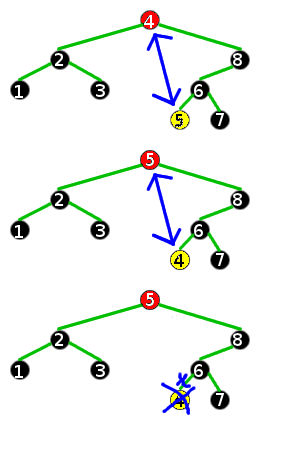













Excellent post.
ReplyDeleteA small typo; "Then you're at the 8, but 8 is less than 5" should read "Then you're at the 8, but 7 is less than 8".
Thanks! I have corrected the typo.
Delete